减治法 是一种一般性的算法设计技术,它利用了一个问题给定实例的解和同样问题较小实例的解之间的关系。一旦建立了这样一种关系,我们既可以自顶至下(递归)也可以自底至上地运用它(非递归)。
减治法有3种主要的变种:
减一个常量 ,常常是减1(例如插入排序)。减一个常因子 ,常常是减去因子2(例如折半查找)。减可变规模 (例如欧几里得算法).
插入排序 是减(减1)治法技术在排序问题上的直接应用。无论平均还是最坏,时间复杂度都是O ( n 2 ) O(n^2) O ( n 2 )
该算法一个较为出众的优势在于,对于几乎有序的数组,它的性能是很好的,最佳情况是O(n)。
代码示例看这里 。
**深度优先查找(DFS)和广度优先查找(BFS)**是两种主要的图遍历算法。
两种算法都有着相同的时间效率:对于邻接矩阵表示法来说是O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
DFS重要的基本应用包括检查图的连通性和无环性。因为DFS在访问了所有和初始顶点有路径相连的顶点之后就会停下来,所以可以检查图的连通性,看看是否所有的顶点都被访问过了。检查无环性则是检查是否有访问过的节点再次被到达。
BFS可以用来求两个给定顶点间边的数量最少的路径。
代码示例看DFS代码 和BFS代码 。两者的比较看这里 。
我们可以用一个代表起点的顶点、一个代表终点的顶点、若干个代表死胡同和通道的顶点来对迷宫建模,迷宫中的通道不止一条,我们必须求出连接起点和终点的迷宫道路。DFS 遍历还是BFS 遍历?
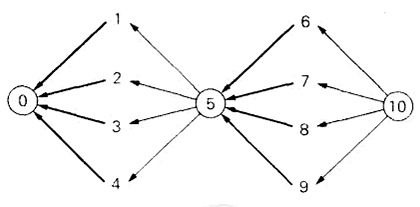
一个有向图 是一个对边指定了方向的图。拓扑排序 要求按照这种次序列出它的顶点,使得对于图中的每一条边来说,边的起始顶点总是排在边的结束顶点之前。当且仅当有向图是一个**无环有向图(不包含回路的有向图)**的时候,该问题有解,也就是说,它不包含有向的回路。
解决拓扑排序问题有两种算法 。第一种算法基于深度优先查找;第二种算法基于减一技术的直接应用,源删除算法。
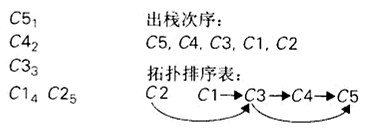
DFS算法 :执行一次DFS遍历,并记住顶点变成死端(即退出遍历栈)的顺序。将该次序反过来就得到了拓扑排序的一个解。
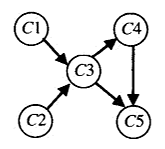
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 #include <iostream> #include <vector> #include <string> #include <unordered_set> #include <algorithm> using namespace std ;class OrderedGraphNode{ public : OrderedGraphNode(string val) : m_val(val){} string get_val () const return m_val;} void add_next (OrderedGraphNode* m) { if (!m) return ; m_nexts.push_back(m); m->add_prev(this ); } std ::vector <OrderedGraphNode*> m_prevs; std ::vector <OrderedGraphNode*> m_nexts; private : string m_val; void add_prev (OrderedGraphNode* m) { if (!m) return ; m_prevs.push_back(m); } }; void dfs (OrderedGraphNode* start, unordered_set <OrderedGraphNode*>& visited, vector <OrderedGraphNode*>& path) if (!start) return ; visited.insert(start); for (auto it = start->m_nexts.begin(); it != start->m_nexts.end(); ++it) { if (*it && visited.count(*it) == 0 ) { dfs(*it, visited, path); } } path.push_back(start); } void find_pre_course (vector <OrderedGraphNode*> classes, vector <OrderedGraphNode*>& result) if (classes.empty()) return ; std ::vector <OrderedGraphNode*> starts; for (auto it = classes.begin(); it != classes.end(); ++it) { if ((*it) && (*it)->m_prevs.empty()) {starts.push_back(*it);} } unordered_set <OrderedGraphNode*> visited; for (auto it = starts.begin(); it != starts.end(); ++it) { dfs(*it, visited, result); } reverse(result.begin(), result.end()); } int main () OrderedGraphNode c1 ("c1" ) ; OrderedGraphNode c2 ("c2" ) ; OrderedGraphNode c3 ("c3" ) ; OrderedGraphNode c4 ("c4" ) ; OrderedGraphNode c5 ("c5" ) ; c1.add_next(&c3); c2.add_next(&c3); c3.add_next(&c4); c3.add_next(&c5); c4.add_next(&c5); OrderedGraphNode* temp[5 ] = {&c1, &c2, &c3, &c4, &c5}; vector <OrderedGraphNode*> classes(temp, temp+5 ); vector <OrderedGraphNode*> result; find_pre_course(classes, result); for_each(result.begin(), result.end(), [](OrderedGraphNode* node){ cout << node->get_val() << " " ;}); cout << endl ; system("Pause" ); }
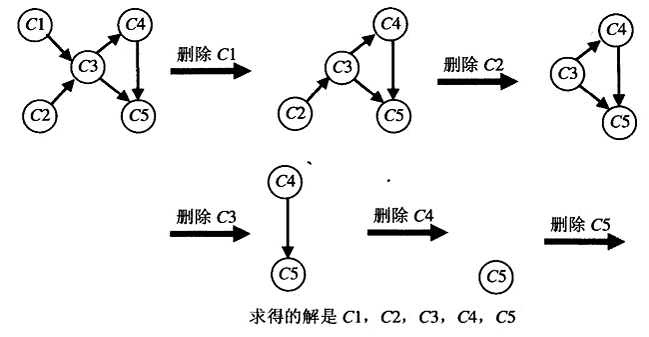
源删除算法 :不断地做这样一件事,在余下的有向图中求出一个源,它是一个没有输入边的顶点,然后把它和所有从它出发的边都删除。(如果有多个这样的源,任选一个。如果没有这样的源,停止,无解)顶点被删除的顺序就是拓扑排序问题的一个解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 #include <iostream> #include <vector> #include <string> #include <unordered_set> #include <algorithm> using namespace std ;class OrderedGraphNode{ public : OrderedGraphNode(string val) : m_val(val){} void delete_me () { for (auto it = m_nexts.begin(); it != m_nexts.end(); ++it) { if (*it) {(*it)->delete_prev(this );} } m_nexts.clear(); } string get_val () const return m_val;} void add_next (OrderedGraphNode* m) { if (!m) return ; m_nexts.push_back(m); m->add_prev(this ); } std ::vector <OrderedGraphNode*> m_prevs; std ::vector <OrderedGraphNode*> m_nexts; private : string m_val; void add_prev (OrderedGraphNode* m) { if (!m) return ; m_prevs.push_back(m); } void delete_prev (OrderedGraphNode* m) { if (!m) return ; m_prevs.erase(remove(m_prevs.begin(), m_prevs.end(), m), m_prevs.end()); } }; void find_pre_course (vector <OrderedGraphNode*> classes, vector <OrderedGraphNode*>& result) if (classes.empty()) return ; while (!classes.empty()) { for (auto it = classes.begin(); it != classes.end(); ++it) { if ((*it) && (*it)->m_prevs.empty()) { result.push_back(*it); (*it)->delete_me(); classes.erase(remove(classes.begin(), classes.end(), *it), classes.end()); break ; } } } } int main () OrderedGraphNode c1 ("c1" ) ; OrderedGraphNode c2 ("c2" ) ; OrderedGraphNode c3 ("c3" ) ; OrderedGraphNode c4 ("c4" ) ; OrderedGraphNode c5 ("c5" ) ; c1.add_next(&c3); c2.add_next(&c3); c3.add_next(&c4); c3.add_next(&c5); c4.add_next(&c5); OrderedGraphNode* temp[5 ] = {&c1, &c2, &c3, &c4, &c5}; vector <OrderedGraphNode*> classes(temp, temp+5 ); vector <OrderedGraphNode*> result; find_pre_course(classes, result); for_each(result.begin(), result.end(), [](OrderedGraphNode* node){ cout << node->get_val() << " " ;}); cout << endl ; system("Pause" ); }
名人问题 。n人人群中的名人是这样定义的:他一个人都不认识,但其他人都认识他。我们的任务是要找出人群中的名人,但只能向人们问这种问题:“你认识他/她吗?”设计一个高效的算法来确定人群中的名人,或者判定人群中没有名人。最坏情况下,该算法要问多少个问题?思路 :通过询问一个问题,每次减少一个人选。递归进行。对最后一人再询问一或两个问题确认。
在设计生成基本组合对象的算法时,减一技术是一种非常自然的选择。这类算法中最高效的类型是最小变化算法。然而,组合对象的数量增长得如此之快,使得实际应用中,即使最高效的算法也只能用来解决这类问题的一些非常小的实例。
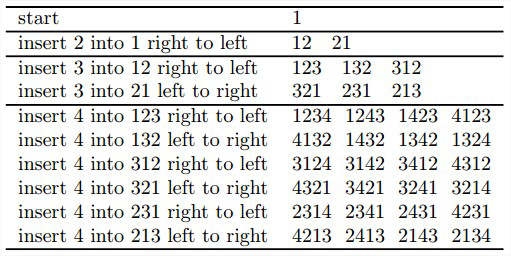
问题:生成{1,…,n}的所有n!个排列。有两种解法,从底至上生成排列算法、Johnson-Trotter算法。
假设(n-1)!个排列的问题已经解决,可以把n插入到n-1个元素的每一种排列中的n个可能位置中去,得到较大规模问题的一个解。最小变化 要求:仅仅需要交换直接前趋中的两个元素就能得到任何一个新的序列。有利于提高算法速度,对使用这些排列的应用也有好处。
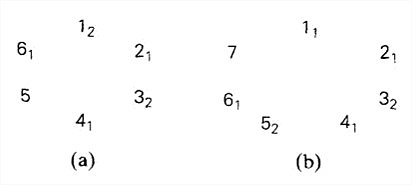
移动元素 的概念。给一个排列中的每个元素k赋予一个方向。用元素上画一个小箭头来表示。如果元素k的箭头指向一个相邻的较小元素,那么它在这个排列中是移动的。
算法思路 :将第一个排列初始化为\overleftarrow1\overleftarrow2...\overleftarrow n。如果仍然存在移动元素k,那么循环:找到最大的移动元素k,把k和它箭头指向的相邻元素互换,调转所有大于k的元素的方向,将新排列添加到列表。
如,对n=3应用该算法:
\overleftarrow1\overleftarrow2\overleftarrow3 \mbox{, } \overleftarrow1\overleftarrow3\overleftarrow2 \mbox{, } \overleftarrow3\overleftarrow1\overleftarrow2 \mbox{, } \overrightarrow3\overleftarrow2\overleftarrow1 \mbox{, } \overleftarrow2\overrightarrow3\overleftarrow1 \mbox{, } \overleftarrow2\overleftarrow1\overrightarrow3
这个算法是生成排列的最有效的算法之一。该算法实现的运行时间和排列的数量是呈正比的,也就是说属于集合O ( n ! ) O(n!) O ( n ! )
这个算法生成的排列的次序不是非常自然。如果是字典序 的话,上述结果应该是:
123\mbox{ }132\mbox{ }213\mbox{ }231\mbox{ }312\mbox{ }321
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <iostream> #include <vector> #include <algorithm> #include <iterator> using namespace std ;struct DirNum{ DirNum(int m) : m_num(m), m_is_left(true ) {} int m_num; bool m_is_left; }; int find_biggest_move_element (const vector <DirNum>& elements) int result (-1 ) int val (INT_MIN) for (int i = 0 ; i < elements.size(); ++i) { if ((elements[i].m_is_left && i != 0 && elements[i].m_num > elements[i-1 ].m_num) || (!elements[i].m_is_left && i != elements.size()-1 && elements[i].m_num > elements[i+1 ].m_num)) { if (elements[i].m_num > val) { val = elements[i].m_num; result = i; } } } return result; } void redirect_bigger_than_this (vector <DirNum>& elements, int val) for (auto it = elements.begin(); it != elements.end(); ++it) { if ((*it).m_num > val) { (*it).m_is_left = !(*it).m_is_left; } } } void johnson_trotter (int n, vector <vector <DirNum> >& result) vector <DirNum> temp; for (int i = 1 ; i < n+1 ; ++i) { DirNum t (i) ; temp.push_back(t); } result.push_back(temp); int big_index (-1 ) while ((big_index = find_biggest_move_element(temp)) > -1 ) { DirNum* me = &temp[big_index]; DirNum* next = me->m_is_left ? &temp[big_index-1 ] : &temp[big_index+1 ]; swap(*me, *next); redirect_bigger_than_this(temp, next->m_num); result.push_back(temp); } } int main () vector <vector <DirNum> > result; johnson_trotter(3 , result); for (auto it = result.begin(); it != result.end(); ++it) { for_each((*it).begin(), (*it).end(), [](DirNum m){cout << m.m_num << "(" << (m.m_is_left ? "←" : "→" ) << ")" << " " ;}); cout << endl ; } system("Pause" ); }
请看这几道leetcode题目。Permutations Permutations II Next Permutation
问题:生成一个抽象集合A=\\{a_1,···,a_2\\}的所有2 n 2^n 2 n
相关题目[Brute Force] | Combinations
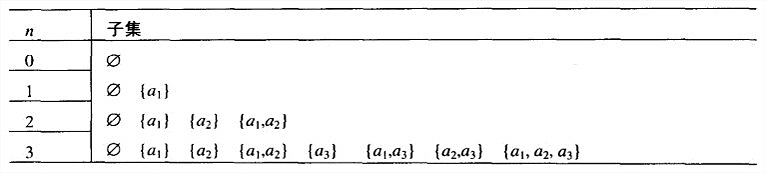
集合A={a1,···,an}的所有子集可以分为两组:不包含an的子集和包含an的子集。前一组就是{a1,…a{n-1}}的所有子集,而后一组中的每个元素都可以通过把an添加到\\{a1,···,a_{n-1}\\}的每一个子集中来获得。
n个元素集合A=\\{a_1,...,a_n\\}的所有2 n 2^n 2 n 2 n 2^n 2 n a i a_i a i b i = 1 b_i=1 b i = 1 a i a_i a i b i = 0 b_i=0 b i = 0
生成的排列次序仍然是很不自然的。挤压序 ,所有包含aj的子集必须紧排在所有包含{a1,…,a j − 1 a_{j-1} a j − 1 二进制反射格雷码 ,每一个比特串和它的直接前趋之间仅仅相差一个比特位。
写一个生成所有2 n 2^n 2 n 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <vector> #include <string> #include <iostream> #include <iterator> using namespace std ;void bit_string_recursive (int n, vector <string >& output, string & cur) if (n == 0 ) { output.push_back(cur); }else { cur.push_back('0' ); bit_string_recursive(n-1 , output, cur); cur.pop_back(); cur.push_back('1' ); bit_string_recursive(n-1 , output, cur); cur.pop_back(); } } int main () vector <string > output; string cur; bit_string_recursive(3 , output, cur); copy(output.begin(), output.end(), ostream_iterator<string >(cout , " " )); cout << endl ; system("Pause" ); }
写一个生成所有2 n 2^n 2 n ,它用数组来实现比特串并且不使用二进制加法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <vector> #include <string> #include <iostream> #include <iterator> using namespace std ;void bit_string_nonrecursive (int n, vector <string >& output) string cur (n,'0' ) int k (n-1 ) while (k >= 0 ) { output.push_back(cur); k = n - 1 ; while (k >= 0 && cur.at(k) == '1' ) {--k;} if (k >= 0 ) { cur[k] = '1' ; for (int i = k+1 ; i < n; ++i) { cur[i] = '0' ; } } } } int main () vector <string > output; bit_string_nonrecursive(3 , output); copy(output.begin(), output.end(), ostream_iterator<string >(cout , " " )); cout << endl ; system("Pause" ); }
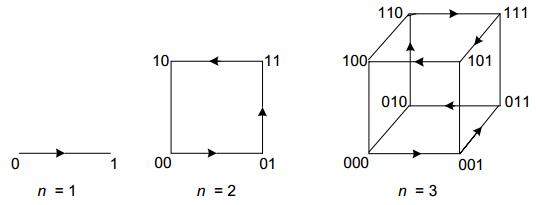
设计一个通用的减一算法来生成次数为n的格雷码 。几何表达方式 ,就是把它的bit值映射到一个n维的立方体上。思路 :得到n-1的输出队列后复制两份。第一份在所有比特序列前加0,第二份在所有比特序列前加1。将第二份反向,添加到第一份的后面,就是n的输出队列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <vector> #include <string> #include <iterator> #include <iostream> #include <algorithm> using namespace std ;void gray_code (int n, vector <string >& output) if (n < 1 ) return ; else if (n == 1 ) { output.push_back("0" ); output.push_back("1" ); }else { gray_code(n-1 , output); vector <string > copy1(output); vector <string > copy2(output); for_each(copy1.begin(), copy1.end(), [](string & n){n = "0" + n;}); for_each(copy2.begin(), copy2.end(), [](string & n){n = "1" + n;}); copy(copy2.rbegin(), copy2.rend(), back_inserter(copy1)); output = copy1; } } int main () vector <string > output; gray_code(3 , output); copy(output.begin(), output.end(), ostream_iterator<string >(cout , " " )); cout << endl ; system("Pause" ); }
另一道关于生成格雷码的题目 。写法上比前面的好。
设计一个减治算法来生成n个元素的k个分量的所有组合 ,也就是说,一个给定的n元素集合的所有k元素子集。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <vector> #include <string> #include <iterator> #include <iostream> #include <algorithm> using namespace std ;void choose_k_of_n (const vector <char >& input, int i, int k, vector <string >& output, string & cur) if (k == 0 ) { output.push_back(cur); }else { for (int j = i; j < input.size() - k + 1 ; ++j) { cur[k-1 ] = input[j]; choose_k_of_n(input, j+1 , k-1 , output, cur); } } } int main () char temp[5 ] = {'A' , 'B' , 'C' , 'D' , 'E' }; vector <char > input(temp, temp+5 ); vector <string > output; string cur; cur.resize(4 ); choose_k_of_n(input, 0 , 4 , output, cur); copy(output.begin(), output.end(), ostream_iterator<string >(cout , " " )); cout << endl ; system("Pause" ); }
格雷码与汉诺塔的相通之处。
减常因子算法的例子有:用天平来辨别假币、俄式乘法、约瑟夫斯问题、折半查找、用平方求幂。
在n枚外观相同的硬币中,有一枚是假币。在一架天平上,我们可以比较任意两组硬币,得知哪一组比另一组更重,但不知道重多少。假币比真币轻。要求设计算法检测这枚假币。
把硬币分成三堆,每堆n/3个硬币更好。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <iostream> #include <vector> using namespace std; // assume fake coin is lighter and there is only one fake coin. int calculate_weight_of_group(const vector<int>& coins, int start, int end) { int weight(0); for (int i = start; i < end; ++i) { weight += coins[i]; } return weight; } //--------------------------------------------------- void find_fake_coin_by_divided_by_3(const vector<int>& coins, int start, int end) { if (start == end-1) // the coin is fake { cout << "fake coin is number " << start << " weight " << coins[start]; }else { // divide the coins into three piles of n/3, n/3, n-2(n/3) coins int div1 = start + (end - start) / 3; int div2 = div1 + (end - start) / 3; // weigh the first two piles int weight1(calculate_weight_of_group(coins, start, div1)); int weight2(calculate_weight_of_group(coins, div1, div2)); if (weight1 == weight2) // if they weigh the same { // discard all of them and continue with the coins of the third pile find_fake_coin_by_divided_by_3(coins, div2, end); }else if (weight1 < weight2) // else continue with the lighter of the first two piles { find_fake_coin_by_divided_by_3(coins, start, div1); }else { find_fake_coin_by_divided_by_3(coins, div1, div2); } } } //--------------------------------------------------- int main() { vector<int> coins(10, 5); coins[7] = 3; find_fake_coin_by_divided_by_3(coins, 0, coins.size()); cout << endl; system("Pause"); }
假设n和m是两个正整数,计算它们的乘积。用n的值作为实例规模的量度。
n × m = n 2 × 2 m n\times m = \frac{n}{2} \times 2m
n × m = 2 n × 2 m
如果n是奇数:
n × m = n − 1 2 × 2 m + m n\times m = \frac{n-1}{2} \times 2m + m
n × m = 2 n − 1 × 2 m + m
通过应用这个公式,并以1 × m = m 1\times m=m 1 × m = m n × m n\times m n × m
例如,用该算法计算5 0 × 6 5 50\times 65 5 0 × 6 5
这个算法使得硬件实现的速度非常快,因为使用移位就可以完成二进制数的折半和加倍。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <iostream> #include <vector> using namespace std ;int russe_nonrecursive (int n, int m) int plus (0 ) while (n != 1 ) { if (n % 2 == 1 ) plus += m; n >>= 1 ; m <<= 1 ; } return plus+m; } int russe_recursive (int n, int m) if (n % 2 == 0 ) {return russe_recursive(n/2 , 2 *m);} else if (n == 1 ) {return m;} else {return russe_recursive((n-1 )/2 , 2 *m) + m;} } int main () cout << "5 * 25 = " << russe_nonrecursive(5 , 25 ) << " solved nonrecursively." << endl ; cout << "5 * 25 = " << russe_recursive(5 , 25 ) << " solved recursively." << endl ; cout << "52 * 78 = " << russe_nonrecursive(52 , 78 ) << " solved nonrecursively." << endl ; cout << "52 * 78 = " << russe_recursive(52 , 78 ) << " solved recursively." << endl ; system("Pause" ); }
让n个人围成一个圈,并将他们从1到n编上号码。从编号为1的那个人那里开始这个残酷的计数,每次消去第二个人直到只留下一个幸存者。问题就是要求算出幸存者的号码J(n)。
可怕的故事!约瑟夫斯是一个著名的犹太历史学家,参与并记录了公元66~70年犹太人反抗罗马的起义。约瑟夫斯作为一个将军,设法守住了裘达伯特的堡垒达47天之久,但在城市陷落了以后,他和40名顽强的将士在附近的一个洞穴中避难。在那里,这些叛乱者表决说“要投降毋宁死”。于是,约瑟夫斯建议每个人应该轮流杀死他旁边的人,而这个顺序是由抽签决定的。约瑟夫斯有预谋地抓到了最后一签,并且,作为洞穴中的两个幸存人之一,他说服了他原来的牺牲品一起投降罗马。
思路 :把奇数n和偶数n情况分开考虑。
如果n为偶数,即n=2k。对整个圆圈处理第一遍之后,生成了同样问题的规模减半的实例。(比如一共4人,初始位置为3的人第2轮会在2号位置上,3=2*2-1。括号里的是本轮的总人数。)唯一差别是位置的编号。同一个人的新旧位置关系是:(旧=2新-1)
J ( 2 k ) = 2 J ( k ) − 1 J(2k)=2J(k)-1
J ( 2 k ) = 2 J ( k ) − 1
如果n为奇数,即n=2k+1。第一轮消去了所有偶数位置上的人。把紧接着消去的位置1上的人也加进来,留下一个规模为k的实例。(比如一共3人,初始位置为3的人第2轮会在1号位置上,3=2*1+1。括号里的是本轮的总人数。)同一个人的新旧位置关系是:(旧=2新+1)
J ( 2 k + 1 ) = 2 J ( k ) + 1 J(2k+1)=2J(k)+1
J ( 2 k + 1 ) = 2 J ( k ) + 1
**一个神奇的解法!**对n本身做一次向左的循环移位得到J(n)。如:J ( 6 ) = J ( 1 1 0 2 ) = 1 0 1 2 = 5 J(6)=J({110}_2)={101}_2=5 J ( 6 ) = J ( 1 1 0 2 ) = 1 0 1 2 = 5 J ( 7 ) = J ( 1 1 1 2 ) = 1 1 1 2 = 7 J(7)=J({111}_2)={111}_2=7 J ( 7 ) = J ( 1 1 1 2 ) = 1 1 1 2 = 7
减可变规模算法 的一次迭代和另一次迭代时消减的规模是变化的。例子如:欧几里得算法、选择问题的基于分区的算法、插值查找和二叉查找树中的查找及插入操作。
选择问题 是求一个n个数列表的第k个最小元素的问题。这个数字被称为第k个顺序统计量。中值 。
中值问题的思路 :先假设s是分区的分割位置。如果s=k,中轴p就是选择问题的解。如果s>k,p是s的左边区域中第k小的元素。如果s<k,p是s的右边区域中第k-s小的元素。从而减小问题规模。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <vector> #include <iostream> #include <algorithm> using namespace std; //--------------------------------------------------- int find_kth_smallest_element(vector<int>& array, int start, int end, int k) { int pivot = array[start]; int left(start+1),right(end); while (left <= right) { while (array[left] <= pivot && left <= right) {++left;} while (array[right] >= pivot && left <= right) {--right;} if (left <= right) { swap(array[left], array[right]); ++left; --right; } } left = min(left, end); right = max(right, start); swap(array[start], array[right]); int partition = right; if (partition > k) { return find_kth_smallest_element(array, start, partition-1, k);} else if (partition < k) {return find_kth_smallest_element(array, partition+1, end, k-partition);} else {return array[partition];} } //--------------------------------------------------- int main() { int temp[5] = {40,30,50,10,20}; vector<int> array(temp, temp+5); cout << "3rd least element in array is : " << find_kth_smallest_element(array, 0, 4, 3-1) << endl; system("Pause"); }
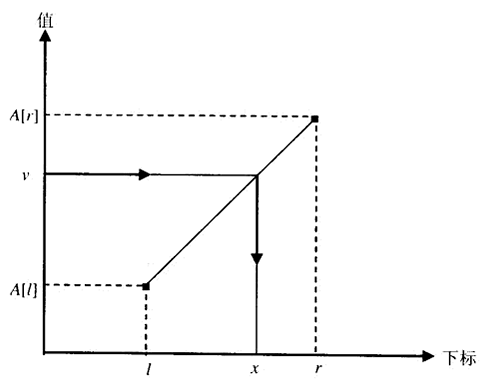
插值查找为了找到用来和查找键进行比较的数组元素,考虑了查找键的值。某种意义上模仿了在电话号码簿上查找名字的方式。如果叫Brown,我们不会翻到号码簿的中间,而是翻到很靠近开头的地方。
r范围内有序,由预查值v带入线性方程求得x。求x实际对应值A(x)。如果A[x]<v,在x+1 r之间找。反之,在l~x-1之间找。
对于较小的文件,折半查找可能更好,但对于更大的文件和那些比较的开销非常大或者访问的成本非常高的应用,插值查找更值得考虑。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <iostream> #include <vector> using namespace std ;int interpolation_search (const vector <int >& datas, int start, int end, int val) int inter = start + ((val - datas[start]) * (end - start) / (datas[end] - datas[start])); if (inter < start || inter > end) return -1 ; if (datas[inter] < val) { return interpolation_search(datas, inter+1 , end, val); }else if (datas[inter] > val) { return interpolation_search(datas, start, inter-1 , val); }else { return inter; } } int main () int temp[10 ] = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 }; vector <int > datas(temp, temp+10 ); cout << "find number " << 7 << " in vector, index: " << interpolation_search(datas, 0 , 9 , 7 ) << endl ; int temp1[10 ] = {1 ,3 ,5 ,7 ,11 ,13 ,17 ,19 ,23 ,29 }; vector <int > datas1(temp1, temp1+10 ); cout << "find number " << 11 << " in vector, index: " << interpolation_search(datas1, 0 , 9 , 11 ) << endl ; system("Pause" ); }
迭代的过程中,树的高度的减少通常不相同,所以是减可变规模算法。讲解和例子见这里 。
其中一个例子是:有一堆n个棋子。两个玩家轮流从堆中拿走最少1个、最多m个棋子。每次拿走的棋子数都可以不同,但能够拿走的上下限数量是不变的。如果每个玩家都做出了最佳选择,哪个玩家能够胜利拿到最后那个棋子?是先走的还是后走的?
扩展为多堆的情况。它的解很奇怪,基于堆中棋子数的二进制表示。b1, b2, …, bn分别是各堆棋子数的二进制表示。求它们的二进制数位和 ,即对每一位分别求和并忽略进位。可以证实,当且仅当二进制数位和中包含至少一个1时,该实例是一个胜局;相反地,当且仅当二进制数位和只包含0的时候,实例是一个败局。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 // 代码写得不算好,寻机修改。 #include <vector> #include <iostream> #include <iterator> #include <algorithm> #include <string> using namespace std; //============================================================ class Robot { public: void pick(vector<int>& piles, int allowed_pick); void single_pick(vector<int>& piles, int allowed_pick); void multi_pick(vector<int>& piles, int allowed_pick); }; //--------------------------------------------------- void Robot::pick( vector<int>& piles, int allowed_pick ) { int no_zero_pile_num(0); for (auto p = piles.begin(); p != piles.end(); ++p) { if (*p){++no_zero_pile_num;} } if (no_zero_pile_num > 1) { multi_pick(piles, allowed_pick); }else { single_pick(piles, allowed_pick); } } //--------------------------------------------------- void Robot::single_pick( vector<int>& piles, int allowed_pick ) { for (int i = 0; i < piles.size(); ++i) { if(!piles[i]) {continue;} int minus(piles[i] % (allowed_pick+1)); // 每次拿走n mod (m+1)个 string helpmsg = minus ? "CalulateSingleRobot(堆,石子): " : "RandomSingleRobot(堆,石子): "; minus = max(1, minus); piles[i] -= minus; cout << helpmsg << i+1 << " " << minus << endl; } } //--------------------------------------------------- void Robot::multi_pick( vector<int>& piles, int allowed_pick ) { unsigned int sum(0); for (auto p = piles.begin(); p != piles.end(); ++p) { sum ^= *p; // 计算多堆的二进制数位和是否为0 } if (sum != 0) // 不为0时是胜局,进行计算 { int index(0); // index是从右向左数,第几位不为0 while (!(sum&(1 << index))) { ++index; } for (int i = 0; i < piles.size(); ++i) { if (piles[i] & (1<<index)) // 当前堆在这个位置上恰好是1,去了这个1。 { int old(piles[i]); piles[i] ^= 1<<index; cout << "CalculateMultiRobot(堆,石子): " << i+1 << " " << old-piles[i] << endl; break; } } }else // 为0时是败局,随机选数 { int pile = rand()%piles.size(); int num = rand()%allowed_pick; piles[pile-1] -= min(piles[pile-1], num); cout << "RandomMultiRobot(堆,石子): " << pile << " " << min(piles[pile-1], num) << endl; } } //============================================================ class Player { public: void pick(vector<int>& piles, int allowed_pick); }; //--------------------------------------------------- void Player::pick( vector<int>& piles, int allowed_pick ) { int pile(0),num(0); auto check = [&]()->bool{ if (pile > piles.size()|| pile == 0 || num > allowed_pick || num > piles[pile-1]) { cout << "重新输入" << endl; return false; } return true; }; cout << "TheTestPlayer(堆,石子): "; cin >> pile >> num; if (!check()) { pick(piles, allowed_pick); }else { piles[pile-1] -= num; } cout << endl; } //============================================================ class Game { public: Game() : m_player_first(false),m_allowed_pick(5),m_player_win(true) {} void start(); void set_piles(vector<int>& piles, int& m_allowed_pick); void print_all_piles(const vector<int>& piles); void main_loop(); bool pile_valid(); void finish(); private: Robot robot; Player player; vector<int> piles; bool m_player_first; bool m_player_win; int m_allowed_pick; }; //--------------------------------------------------- void Game::set_piles( vector<int>& piles, int& m_allowed_pick ) { cout << "欢迎进行拈游戏,请输入每堆石子情况,空格隔开,-1结束。" << endl; piles.clear(); int num(0); while(cin >> num && num != -1) { piles.push_back(num); } cout << "输入每次最多拿几个石子。" << endl; cin >> m_allowed_pick; } //--------------------------------------------------- void Game::print_all_piles( const vector<int>& piles ) { cout << "---"; copy(piles.begin(), piles.end(), ostream_iterator<int>(cout, "---")); cout << endl; } //--------------------------------------------------- void Game::start() { cout << "==========================================" << endl; set_piles(piles, m_allowed_pick); cout << "开始玩拈游戏,你先手?输入Y或N。" << endl; string temp("N"); cin >> temp; if (temp == "Y" || temp == "y") { m_player_first = true; }else { m_player_first = false; } } //--------------------------------------------------- void Game::main_loop() { while (true) { if (m_player_first) { player.pick(piles, m_allowed_pick); print_all_piles(piles); if (!pile_valid()) {m_player_win = true; break;} robot.pick(piles, m_allowed_pick); print_all_piles(piles); if (!pile_valid()) {m_player_win = false; break;} }else { robot.pick(piles, m_allowed_pick); print_all_piles(piles); if (!pile_valid()) {m_player_win = false; break;} player.pick(piles, m_allowed_pick); print_all_piles(piles); if (!pile_valid()) {m_player_win = true; break;} } } } //--------------------------------------------------- bool Game::pile_valid() { int pile_count(0); for_each(piles.begin(), piles.end(), [&](int p){if (p) pile_count+=p;}); if (pile_count == 0) {return false;} return true; } //--------------------------------------------------- void Game::finish() { if (m_player_win){cout << "玩家胜利!" << endl;} else{cout << "机器胜利!" << endl;} } //============================================================ int main() { Game game; while(true) { game.start(); game.main_loop(); game.finish(); } system("Pause"); }
另类单堆拈游戏 规定谁拿走最后一个棋子就输了。该游戏的其他条件都不变,即该堆棋子有n个,每次每个玩家最多拿走m个,最少拿走1个。请指出游戏的胜局和败局是是怎样的?答案 :败局是n mod (m+1) = 1,胜利的策略是每次拿走(n-1) mod (m+1)的棋子。
坏巧克力 。两个玩家轮流掰一块m × n m\times n m × n 1 × 1 1 \times 1 1 × 1 答案 :相当于多堆拈游戏,每边到达坏巧克力块的距离就是一堆,然后二进制数位和计算。
翻薄饼 。有n张大小互不相同的薄饼,一张叠在另一张上面。允许大家把一个翻板插到一个薄饼下面,然后可以把板上面的这叠薄饼翻个身。我们的目标是根据薄饼的大小重新安排它们的位置,最大的饼要放在最下面。答案 :找到最大的,翻到顶,然后全部翻过来。重复。
[1] 算法设计与分析基础(第2版)




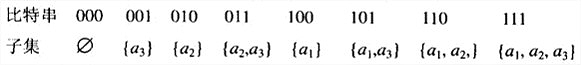
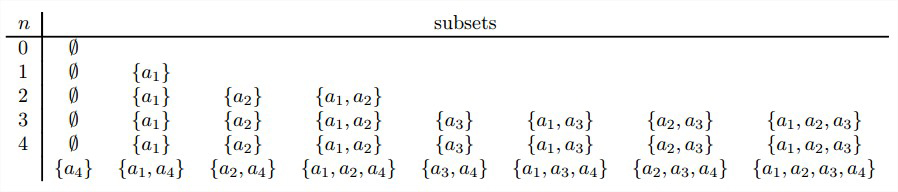
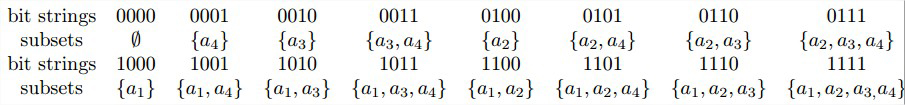

![x的计算方程,即穿越点(l,A[l])和点(r,A[r])直线的标准方程(相似三角形)](/img/insert_search_x_formula.png)