Graph

A Stellar Hiker

2015-01-11

图简介

图由顶点和连接它们的边组成。如果边是有方向的，就是有向图；如果边没有方向，就是无向图。
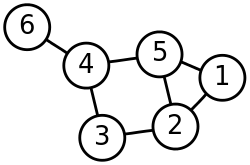
一个无向图

图的遍历

深度优先搜索(Depth-First Search)

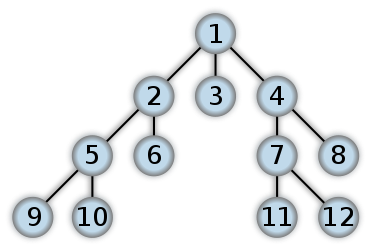
图的深度优先搜索遍历类似于树的前序遍历。它的基本思想是：从图G的某个顶点v0出发，访问v0，然后选择一个与v0相邻且没被访问过的顶点v1访问，再从v1出发选择一个与v1相邻且未被访问的顶点v进行访问，依次继续。如果当前被访问过的顶点的所有邻接顶点都已被访问，则退回到已被访问的顶点序列中最后一个拥有未被访问的相邻顶点的顶点w，从w出发按同样的方法向前遍历，直到图中所有顶点都被访问。
与树先序遍历不同之处在于必须检查节点是否已经访问过。
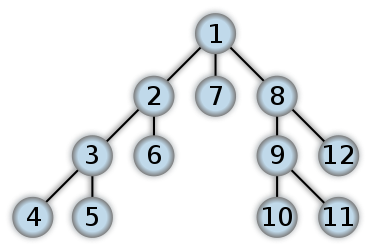
Order in which the nodes are expanded

#include <vector>
#include <unordered_set>
#include <iostream>
class UndirectedGraphNode
{
public:
	int label;
	std::vector<UndirectedGraphNode*> neighbors;
	UndirectedGraphNode(int x) : label(x){}
	void add_to_neighbor(UndirectedGraphNode* node) {neighbors.push_back(node);}
};
void DFS_search(UndirectedGraphNode* root, std::unordered_set<UndirectedGraphNode*>& visited)
{
	if (!root) {return;}
	std::cout << root->label << " ";
	visited.insert(root);
	for (std::vector<UndirectedGraphNode*>::iterator it = root->neighbors.begin(); it != root->neighbors.end(); ++it)
	{
		if (!visited.count(*it))
		{
			DFS_search(*it, visited);
		}
	}
}
int main()
{
	UndirectedGraphNode n1(1);
	UndirectedGraphNode n2(2);
	UndirectedGraphNode n3(3);
	UndirectedGraphNode n4(4);
	UndirectedGraphNode n5(5);
	UndirectedGraphNode n6(6);
	n1.add_to_neighbor(&n2);
	n1.add_to_neighbor(&n5);
	n2.add_to_neighbor(&n1);
	n2.add_to_neighbor(&n5);
	n2.add_to_neighbor(&n3);
	n3.add_to_neighbor(&n2);
	n3.add_to_neighbor(&n4);
	n4.add_to_neighbor(&n3);
	n4.add_to_neighbor(&n5);
	n4.add_to_neighbor(&n6);
	n5.add_to_neighbor(&n1);
	n5.add_to_neighbor(&n2);
	n5.add_to_neighbor(&n4);
	n6.add_to_neighbor(&n4);
	std::unordered_set<UndirectedGraphNode*> visited;
	DFS_search(&n1, visited);
	system("Pause");
}

广度优先搜索(Breadth-First Search)

图的广度优先搜索是树的按层次遍历的推广。它的基本思想是：首先访问初始点vi，并将其标记为已访问过，接着访问vi的所有未被访问过的邻接点vi1, vi2, …, vit，并均标记为已访问过，然后再按照vi1, vi2, …, vit的顺序，访问每一个顶点的所有未被访问过的邻接点，并均标记为已访问过，以此类推，直到图中所有和初始点vi有路径相同的顶点都被访问过为止。
不是递归的。分层的。不会回退。需要辅助队列。
广度优先搜索
Order in which the nodes are expanded

#include <vector>
#include <unordered_set>
#include <iostream>
#include <queue>
class UndirectedGraphNode
{
public:
	int label;
	std::vector<UndirectedGraphNode*> neighbors;
	UndirectedGraphNode(int x) : label(x){}
	void add_to_neighbor(UndirectedGraphNode* node) {neighbors.push_back(node);}
};
void BFS_search(UndirectedGraphNode* root, std::unordered_set<UndirectedGraphNode*>& visited)
{
	if (!root) {return;}
	std::queue<UndirectedGraphNode*> nodes;
	std::cout << root->label << " ";
	visited.insert(root);
	nodes.push(root);
	while (!nodes.empty())
	{
		UndirectedGraphNode* node = nodes.front();
		nodes.pop();
		for (std::vector<UndirectedGraphNode*>::iterator it = node->neighbors.begin(); it != node->neighbors.end(); ++it)
		{
			if (visited.count(*it)) continue;
			std::cout << (*it)->label << " ";
			visited.insert(*it);
			nodes.push(*it);
		}
	}
}
int main()
{
	UndirectedGraphNode n1(1);
	UndirectedGraphNode n2(2);
	UndirectedGraphNode n3(3);
	UndirectedGraphNode n4(4);
	UndirectedGraphNode n5(5);
	UndirectedGraphNode n6(6);
	n1.add_to_neighbor(&n2);
	n1.add_to_neighbor(&n5);
	n2.add_to_neighbor(&n1);
	n2.add_to_neighbor(&n5);
	n2.add_to_neighbor(&n3);
	n3.add_to_neighbor(&n2);
	n3.add_to_neighbor(&n4);
	n4.add_to_neighbor(&n3);
	n4.add_to_neighbor(&n5);
	n4.add_to_neighbor(&n6);
	n5.add_to_neighbor(&n1);
	n5.add_to_neighbor(&n2);
	n5.add_to_neighbor(&n4);
	n6.add_to_neighbor(&n4);
	std::unordered_set<UndirectedGraphNode*> visited;
	BFS_search(&n1, visited);
	system("Pause");
}

DFS与BFS比较

空间复杂度均为O(n)，借用堆栈或队列。
BSF常用在比较大的树上。

DFS和BFS的主要性质

最小生成树问题

n个顶点的有权图可以生成很多不同的生成树，其中生成后树上各边权值之和最小的树就是最小生成树。
连通图的一棵生成树是包含图的所有顶点的连通无环子图(也就是一棵树)。加权连通图的一棵最小生成树是图的一棵权重最小的生成树，其中，树的权重定义为所有边的权重总和。最小生成树问题就是求一个给定的加权连通图的最小生成树问题。

普里姆算法(Prim)

V是所有的顶点，U是已经在最小生成树中的顶点，选择在U和V-U中各有一个顶点的代价最小的边加入最小生成树，同时将该边未收录的顶点加入U。如此重复，直到U=V为止。
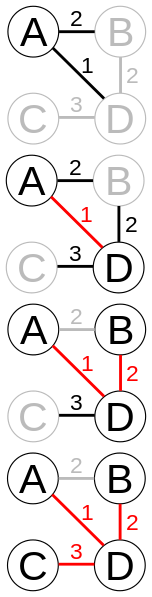
Prim's Algorithm
是一种贪婪算法。
一步一步归并点，找两个阵营之间最小的边，适合稠密图。

#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
using namespace std;
//=============================================================
// 有向图定义
class Vertex;
class Edge
{
public:
	Edge(Vertex* i, Vertex* v, int cost);
	Vertex* get_income_vertex() {return m_income_vertex;}
	Vertex* get_next_vertex(){return m_next_vertex;}
	int get_cost() {return m_cost;}
protected:
	Vertex* m_income_vertex;
	Vertex* m_next_vertex;
	int m_cost;
};
//---------------------------------------------------
class Vertex
{
public:
	Vertex(char data):m_data(data){}
	void add_edge(Edge* e) {if (!e) {return;} m_edges.push_back(e);}
	void erase_edge(Edge* e){m_edges.remove(e);}
	Edge* get_smallest_edge_connect_to_other(vector<Vertex*> collection)
	{
		m_edges.sort([](Edge* a, Edge* b) {return a->get_cost() < b->get_cost();});
		for (auto it = m_edges.begin(); it != m_edges.end(); ++it)
		{
			if (find(collection.begin(), collection.end(), (*it)->get_next_vertex()) == collection.end())
			{
				return *it;
			}
		}
		return NULL;
	}
	char get_data() {return m_data;}
	int get_edge_num() {return m_edges.size();}
	void clear_edge() {m_edges.clear();}
protected:
	char m_data;
	list<Edge*> m_edges;
};
//---------------------------------------------------
Edge::Edge( Vertex* i, Vertex* v, int cost ):m_income_vertex(i),m_next_vertex(v),m_cost(cost)
{
	m_income_vertex->add_edge(this);
}
//---------------------------------------------------
class Graph
{
public:
	void add_vertex(Vertex* v) {m_vertexes.push_back(v);}
	Vertex* get_front_vertex() {return *m_vertexes.begin();}
	void pop_front_vertex() {m_vertexes.erase(m_vertexes.begin());}
	vector<Vertex*> m_vertexes;
};
//=============================================================
void prim(Graph& graph, vector<Vertex*>& tree_vertexes, vector<Edge*>& tree_edge)
{
	// 构造最小生成树的Prim算法
	// 输入：加权连通图graph
	// 输出：tree组成graph的最小生成树
	tree_vertexes.push_back(graph.get_front_vertex());
	graph.pop_front_vertex();
	int size(0);
	while (tree_vertexes.size() != size)
	{
		size = tree_vertexes.size();
		Edge* pe(NULL);
		int cost(INT_MAX);
		for (auto it = tree_vertexes.rbegin(); it != tree_vertexes.rend(); ++it)
		{
			Edge* t = (*it)->get_smallest_edge_connect_to_other(tree_vertexes);
			if (t && t->get_cost() < cost)
			{
				pe = t;
				cost = t->get_cost();
			}
		}
		if (pe)
		{
			tree_edge.push_back(pe);
			tree_vertexes.push_back(pe->get_next_vertex());
		}
	}
}

//=============================================================
int main()
{
	Vertex v1('a');
	Vertex v2('b');
	Vertex v3('c');
	Vertex v4('d');
	Edge e1(&v1, &v2, 2);
	Edge e2(&v2, &v1, 2);
	Edge e3(&v2, &v4, 2);
	Edge e4(&v4, &v2, 2);
	Edge e5(&v1, &v4, 1);
	Edge e6(&v4, &v1, 1);
	Edge e7(&v3, &v4, 3);
	Edge e8(&v4, &v3, 3);
	Graph g;
	g.add_vertex(&v1);
	g.add_vertex(&v2);
	g.add_vertex(&v3);
	g.add_vertex(&v4);
	vector<Vertex*> tree_vertexes;
	vector<Edge*> tree_edges;
	prim(g, tree_vertexes, tree_edges);
	for_each(tree_edges.begin(), tree_edges.end(), [](Edge* e){
		cout << e->get_income_vertex()->get_data() << " -> " << e->get_next_vertex()->get_data() << endl;
	});
	system("Pause");
}

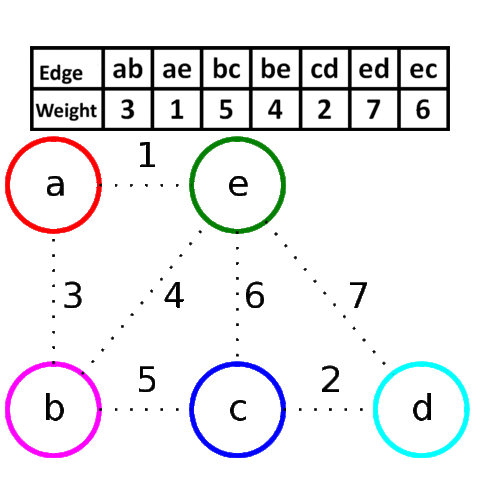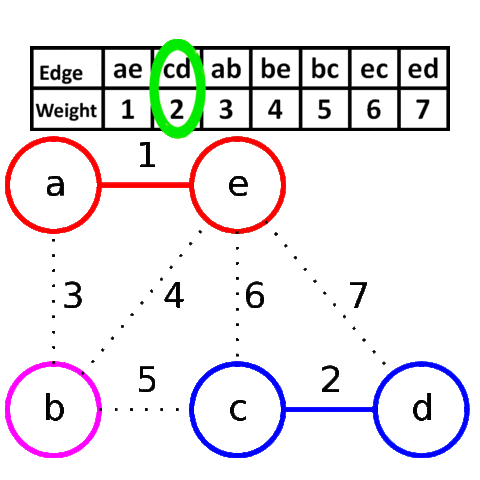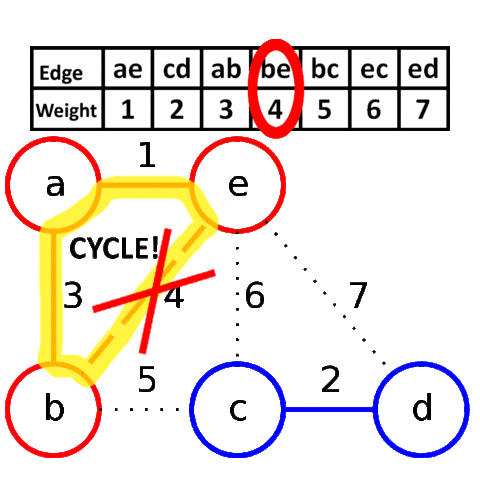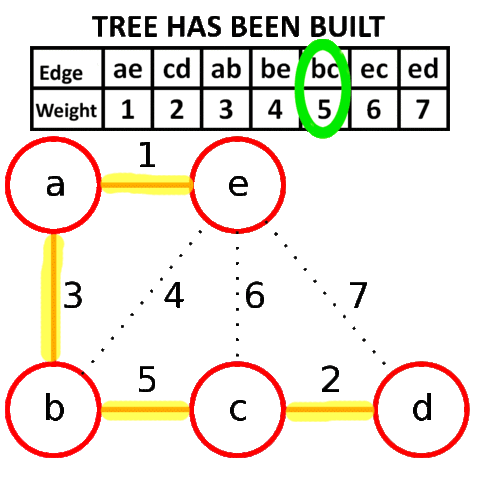
克鲁斯卡尔算法(Kruskal)

V是所有的顶点，让最小生成树的初始状态为包括所有顶点却没有边，每一个顶点是一个连通分量。选择代价最小的边，如果边的两边属于同一个连通分量就放弃，否则加入。边连接的两边变成一个连通分量。如此重复，直到图中所有的顶点都在同一连通分量上。
Kruskal's Algorithm
是一种贪婪算法。
一步一步添加边，找最小的边作为桥梁连通另一个阵营，适合稀疏图。

不相交子集和并查算法

Kruskal算法中用来判断两个顶点是否属于同一连通分量的算法称为union-find(并查)算法。
需要得到的是这样一种抽象数据类型，它是由某个有限集的一系列不相交子集以及下面这些操作构成的：

makeset(x) 生成一个单元素集合{x}。假设这个操作对集合S的每一个元素只能应用一次。
find(x) 返回一个包含x的子集。
union(x,y) 构造分别包含x和y的不相交子集 $S_x$ 和 $S_y$ 的并集，并把它添加到子集的集合中，以代替被删除后的 $S_x$ 和 $S_y$ 。

举例：S={1,2,3,4,5,6}。6次makeset(i)后得到：{1},{2},{3},{4},{5},{6}。执行union(1,4)和union(5,2)后得到：{1,4},{5,2},{3},{6}。再执行union(4,5)和union(3,6)后得到{1,4,5,2},{3,6}。

实现这种数据结构有两种主要的做法。第一种称为快速查找，其查找操作的时间效率是最优的；第二种称为快速求并，其求并集操作是最优的。

快速查找使用一个数组，并以集合S中的元素来索引数组；数组中的值指出了包含这些元素的子集代表。每一个子集都是链表实现的，表头包含了指向表头和表尾元素的指针以及表中的元素个数。
于是，makeset(x)的实现是把代表数组中相应元素的值赋为x，并把相应的链表初始化为值为x的单节点链表，O(1)。find(x)是从代表数组中取出x的代表，O(1)。union(x,y)的一种直接的做法就是简单地把y的列表添加到x列表后面，对于y列表中的所有元素更新它们的代表信息，然后再删除y的列表，O(n^2)。
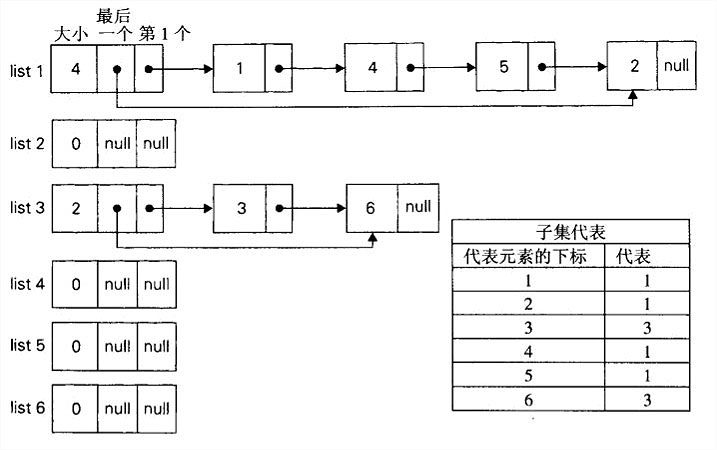
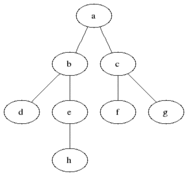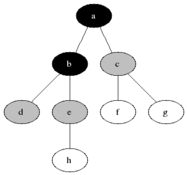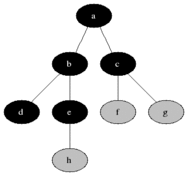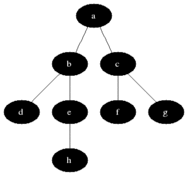
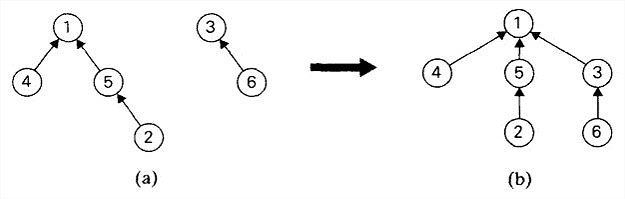
快速求并用一棵有根树来表示每一个子集。树中的节点包含子集中的元素(每个节点一个元素)，而根中的元素就被当做该子集的代表；树中的边从子女指向它们的父母。(此外，还要维护一个从集合元素到树中节点的映射，比如说用一个指针数组来实现。未在下图中显示。)
于是，makeset(x)需要创建一棵单节点的树，O(1)，初始化n棵单节点的树是O(n)。union(x,y)是把y树的根附加到x树的根上(并把指向y树的根的指针置为空，来把y树删除)，O(1)。find(x)需要沿着一条指针链，从包含x的节点开始找到树的根(根中元素作为子集代表就是该函数的返回值)，O(n)。

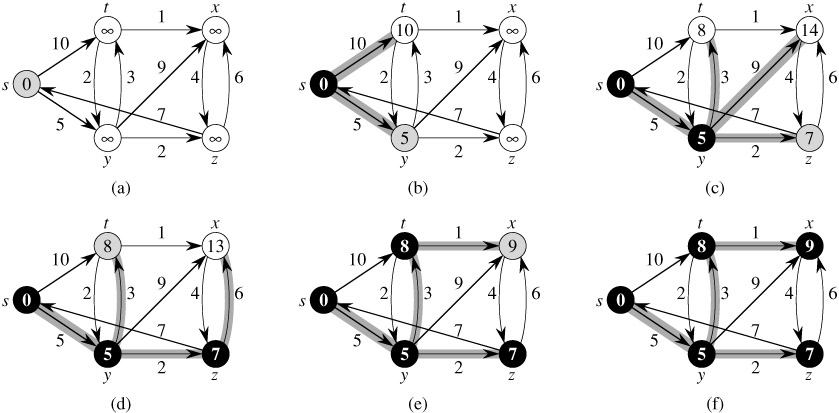
最短路径之德杰斯特拉算法(Dijkstra)

德杰斯特拉算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
Dijkstra算法只能应用于不含负权重的图。
Dijkstra算法能得到最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。
其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时，S中只有起点。设u是S之外的一个顶点。把从起点到u且中间只经过S中顶点的路称为从起点到u的特殊路径，并记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将其添加到S中，并根据新的S集合，对其他顶点的最短路径长度进行更新。当S=V时，就得到了从起点到所有其他顶点之间的最短路径长度。
Dijkstra's Algorithm

1
2