Tree

A Stellar Hiker

2015-01-10

树简介

一棵树的逻辑很简单：除了根节点之外每个节点只有一个父节点，根节点没有父节点；除了叶节点之外所有节点都有一个或多个子节点，叶节点没有子节点。父节点和子节点之间用指针链接。

注意区分的一些概念

二叉树(Binary Tree)

二叉树的特点是每个节点至多只有两棵子树，并且子树有左右之分，次序不能任意颠倒。

在二叉树的第i层上至多有 $2^{i-1}$ 个节点( $i\geqslant1$ )。
深度为k的二叉树至多有 $2^k-1$ 个节点( $k\geqslant1$ )。
对任何一棵二叉树T，如果其终端节点数为 $n_0$ ，度为2的节点数为 $n_2$ ，则 $n_0= n_2+1$ 。

二叉树的前序遍历(pre-order)

先访问根节点，再访问左子节点，最后访问右子节点。
递归方法最直接简单，也可以用迭代的方法。
代码示例可见相关题目Binary Tree Preorder Traversal。

二叉树的中序遍历(in-order)

先访问左子节点，再访问根节点，最后访问右子节点。
递归方法最直接简单，也可以用迭代的方法。
代码示例可见相关题目Binary Tree Inorder Traversal。

二叉树的后序遍历(post-order)

先访问左子节点，再访问右子节点，最后访问根节点。
递归方法最直接简单，也可以用迭代的方法。
代码示例可见相关题目Binary Tree Postorder Traversal。

二叉查找树(Binary Search Tree)

Binary Search Tree
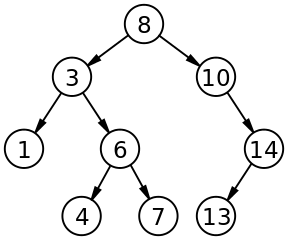
二叉查找树中，左子树的节点总是小于或等于根节点，右子树的节点总是大于或等于根节点。

可以在平均O(logn)的时间内根据数值在二叉查找树中找到一个节点。最坏情况时O(n)。

判断是否是二叉查找树

左子树是二叉查找树，右子树也是二叉查找树，左节点<自己<右节点。
最直观就是用递归，代码看相关题目Validate Binary Search Tree。

在二叉查找树中查找一个元素

递归与迭代两种方法。

#define NULL 0
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode* find_in_BST_recursive(TreeNode* root, int key)
{
	if (!root || root->val == key) {return root;}
	else if (key < root->val) {return find_in_BST_recursive(root->left, key);}
	else {return find_in_BST_recursive(root->right, key);	}
}
TreeNode* find_in_BST_iterative(TreeNode* root, int key)
{
	TreeNode* node = root;
	while (node)
	{
		if (node->val == key) {return node;}
		else if (node->val > key) {node = node->left;}
		else {node = node->right;}
	}
	return NULL;
}
int main()
{
	TreeNode* root1 = NULL;
	TreeNode* result1 = find_in_BST_recursive(root1, 5);
	TreeNode* result2 = find_in_BST_iterative(root1, 5);
	TreeNode root2(5);
	result1 = find_in_BST_recursive(&root2, 5);
	result2 = find_in_BST_iterative(&root2, 5);
	TreeNode root3(3);
	TreeNode lnode(1);
	root3.left = &lnode;
	root3.right = &root2;
	result1 = find_in_BST_recursive(&root3, 5);
	result2 = find_in_BST_iterative(&root3, 5);
	result1 = find_in_BST_recursive(&root3, 2);
	result2 = find_in_BST_iterative(&root3, 2);
}

向二叉查找树中插入一个元素

递归方式，依旧是查找的过程，走到它应该的位置却是NULL的时候就插入。
注意生成的二叉查找树的结构和插入顺序相关。

void insert_in_BST_recursive(TreeNode*& root, int data)
{
	if (!root) {root = new TreeNode(data);}
	else if (data < root->val) {insert_in_BST_recursive(root->left, data);}
	else {insert_in_BST_recursive(root->right, data);}
}

从二叉查找树中删除一个元素

如果删除的节点是：

叶子节点：直接删除。
有一个孩子的节点：删除它，替换为它的孩子。
有两个孩子的节点：让该节点中序遍历时的下一节点(或上一节点)来顶上。如此递归下去直到遇到前两种情况。
第三种情况如图：

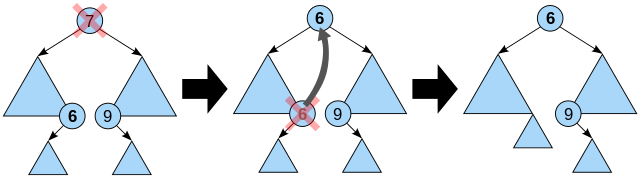
// TreeNode没有指向父节点的指针，所以需要一个表来管理，代码不太好看。
// 死心眼，可以只交换值啊，干嘛非要动节点。
#include <unordered_map>
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode* find_min_in_tree(TreeNode* root, std::unordered_map<TreeNode*, TreeNode*>& parent_map)
{
	if (!root) return NULL;
	TreeNode* node = root;
	while (node->left)
	{
		parent_map.insert(std::make_pair(node->left, node));
		node = node->left;
	}
	return node;
}
TreeNode* replace_in_parent(TreeNode* node, TreeNode* newnode, const std::unordered_map<TreeNode*, TreeNode*>& parent_map)
{
	TreeNode* parent = parent_map.at(node);
	if (!parent) return newnode;
	if (parent->left == node){parent->left = newnode;}
	else{parent->right = newnode;}
	return newnode;
}
TreeNode* remove_in_BST(TreeNode*& root, int key, std::unordered_map<TreeNode*, TreeNode*>& parent_map)
{
	if (!root) {return root;}
	if (root->left) {parent_map.insert(std::make_pair(root->left, root));}
	if (root->right) {parent_map.insert(std::make_pair(root->right, root));}
	if (key < root->val) {root->left = remove_in_BST(root->left, key, parent_map);}
	else if (key > root->val) {root->right = remove_in_BST(root->right, key, parent_map);}
	else
	{
		if (root->left && root->right)
		{
			TreeNode* successor = find_min_in_tree(root->right, parent_map);
			root->val = successor->val;
			remove_in_BST(successor, successor->val, parent_map);
		}else if (root->left)
		{
			root = replace_in_parent(root, root->left, parent_map);
		}else if (root->right)
		{
			root = replace_in_parent(root, root->right, parent_map);
		}else
		{
			root = replace_in_parent(root, NULL, parent_map);
		}
	}
	return root;
}

平衡二叉树(Balanced Binary Tree)

如果树不平衡，在描述时间复杂度的时候，平均和最坏情况都要说明。
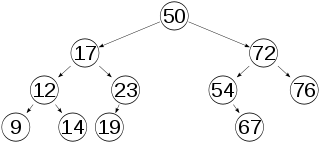
Balanced Tree
平衡树是空树或具有以下性质的二叉树：它的左子树和右子树的深度之差的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

二叉平衡树的诞生是为了更高效的查询。一般的二叉查找树的查询复杂度是跟目标节点到树根的距离(即深度)有关，因此当节点的深度普遍较大时，查询的均摊复杂度会上升，平衡二叉树就应运而生了。
实现一棵平衡树有很多种方法，如2-3 tree, AA tree, AVL tree, Red-Black tree, Scapegoat tree, Splay tree, Treap。
以AVL tree和Red-Black tree为例。

AVL tree

基本操作 $\approx$ 普通二叉树该操作 $+$ 0或几次tree rotation。
平衡因子Balance Factor为：该节点的左子树的深度减去它右子树的深度。平衡二叉树的所有节点的平衡因子只可能为-1, 0或1。

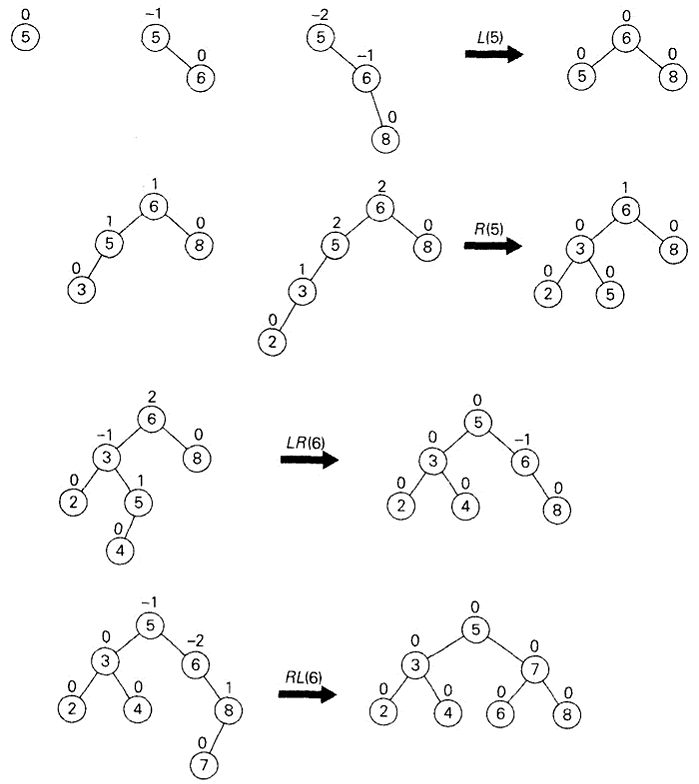
Tree Rotation用来让树重新获得平衡。
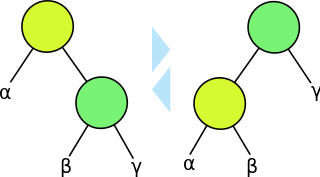
Tree Rotations
四种情况

Left Left Case: 插入点为左子树的左孩子，向右旋转。
Right Right Case: 插入点为右子树的右孩子，向左旋转。
Left Right Case: 插入点为左子树的右孩子，要进行两次旋转，先左旋转，再右旋转。第一次最小不平衡子树的根节点不动，调整插入节点所在的子树，第二次再调整最小不平衡树。
Right Left Case: 插入点为右子树的左孩子，要进行两次旋转，先右旋转，再左旋转。与Left Right Case类似。

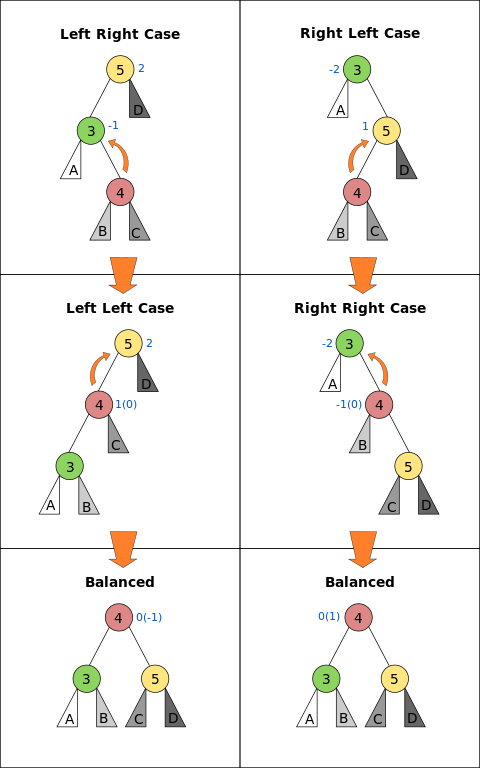
How AVL Tree Reblance.数字编号圆圈表示正在平衡的节点。字母编号三角表示已平衡的子树。节点旁的蓝色数字表示可能的平衡因子

请记住，如果有若干个节点的平衡因子为 $2$ ，先找出最靠近新插入的叶子的不平衡节点，然后再旋转以该节点为根的树。
通过连续的插入，为列表5,6,8,3,2,4,7构造一棵AVL树。旋转缩写旁边的括号中的数字，指出了被重新组织的树的根

1	// 构造一棵AVL树

AVL树的缺点是频繁的旋转、需要维护树的节点的平衡以及总体上的复杂性，尤其是删除操作。

Red-Black tree

STL库中的set/multiset/map/multimap等是基于红黑树实现的。
红黑树并不严格平衡，但足够保证查找时O(logn)时间复杂度。
红黑树的叶节点不包含数据。
从根到叶子的最长的可能路径不超过最短的可能路径的两倍长。（最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点）于是树大致是平衡的。

An Example of a Red-Black Tree
性质：

1.节点是红色或黑色。
2.根节点是黑色的。
3.叶节点都是黑色的(叶节点是NIL节点)。
4.每一个红色的节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
5.从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

注意：

性质1和3总是保持着。
性质4只在增加红色节点、重绘黑色节点为红色，或做旋转时受到威胁。
性质5只在增加黑色节点、重绘红色节点为黑色，或做旋转时受到威胁。

插入

首先以二叉查找树的方法增加节点并标记为红色。之后注意要保持红黑树的特性：

情形1：新节点N位于树的根上，没有父节点。此时把它重绘为黑色满足性质2。因为它在每个路径上对黑节点数目+1，性质5符合。
情形2：新节点的父节点P是黑色，所以性质4没有失效。此时，树仍是有效的。
注意：在下列情形下我们假定新节点的父节点为红色，所以它有祖父节点；因为如果父节点是根节点，那父节点就应当是黑色。所以新节点总有一个叔父节点，尽管在情形4和5下它可能是叶子节点。
情形3：如果父节点P和叔父节点U也是红色，那么可以把它们两个重绘为黑色并重绘爷爷节点G为红色。爷爷节点G的父节点也可能是红色的，不符合性质4，所以此时需要从头开始整个过程，把G当成新加入的节点进行各种情形的检查。

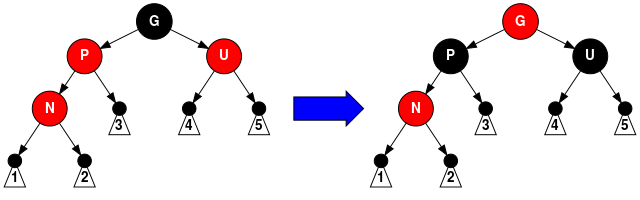
注意：在余下的情形下，我们假定父节点P是其父亲G的左子节点。如果它是右子节点，情形4和情形5中的左和右应当对调。
情形4：父节点P是红色而叔父节点U是黑色或缺少，并且新节点N是其父节点P的右子节点而父节点P又是其父节点的左子节点。在这种情形下，我们进行一次左旋转调换新节点和其父节点的角色; 接着，我们按情形5处理以前的父节点P以解决仍然失效的性质4。
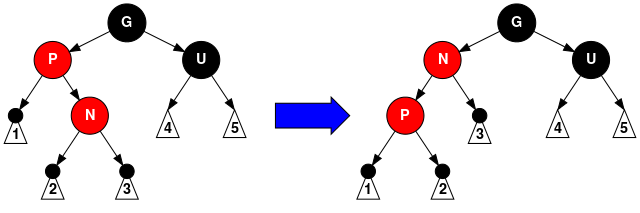
情形5：父节点P是红色而叔父节点U是黑色或缺少，新节点N是其父节点的左子节点，而父节点P又是其父节点G的左子节点。在这种情形下，我们进行针对祖父节点G的一次右旋转; 在旋转产生的树中，以前的父节点P现在是新节点N和以前的祖父节点G的父节点。我们知道以前的祖父节点G是黑色，否则父节点P就不可能是红色(如果P和G都是红色就违反了性质4，所以G必须是黑色)。我们切换以前的父节点P和祖父节点G的颜色，结果的树满足性质4。

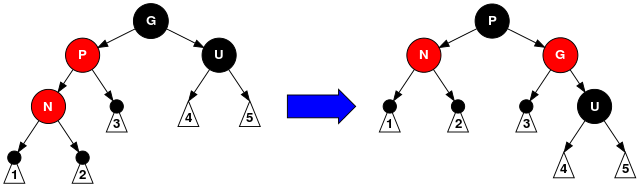
删除

如果需要删除的节点有两个儿子，那么问题可以被转化成删除另一个只有一个儿子的节点的问题（为了表述方便，这里所指的儿子，为非叶子节点的儿子）。对于二叉查找树，在删除带有两个非叶子儿子的节点的时候，我们找到要么在它的左子树中的最大元素、要么在它的右子树中的最小元素，并把它的值转移到要删除的节点中(如在这里所展示的那样)。我们接着删除我们从中复制出值的那个节点，它必定有少于两个非叶子的儿子。因为只是复制了一个值，不违反任何性质，这就把问题简化为如何删除最多有一个儿子的节点的问题。它不关心这个节点是最初要删除的节点还是我们从中复制出值的那个节点。

于是可以只讨论删除只有一个儿子的节点的问题。
如果我们删除一个红色节点，它的父亲和儿子一定是黑色的。所以我们可以简单的用它的黑色儿子替换它，并不会破坏性质3和性质4。通过被删除节点的所有路径只是少了一个红色节点，这样可以继续保证性质5。
如果我们删除一个黑色节点，且它的儿子是红色的。只需删除它，用它的红色儿子顶替上来并重绘为黑色。

当要删除的节点和它的儿子都是黑色时，首先把要删除的节点替换为它的儿子。出于方便，称呼这个儿子为N(在新的位置上)，称呼它的兄弟(它父亲的另一个儿子)为S。在下面的示意图中，我们还是使用P称呼N的父亲，SL称呼S的左儿子，SR称呼S的右儿子。
如果N和它初始的父亲是黑色，则删除它的父亲导致通过N的路径都比不通过它的路径少了一个黑色节点。因为这违反了性质5，树需要被重新平衡。

比较复杂，有多种情形：

情形1：N是新的根。此时所有性质都保持着，完成。
注意：在情形2、5和6下，我们假定N是它父亲的左儿子。如果它是右儿子，则在这些情形下的左和右应当对调。
情形2：S是红色。在这种情形下我们在N的父亲上做左旋转，把红色兄弟转换成N的祖父，我们接着对调N的父亲和祖父的颜色。完成这两个操作后，尽管所有路径上黑色节点的数目没有改变，但现在N有了一个黑色的兄弟和一个红色的父亲（它的新兄弟是黑色因为它是红色S的一个儿子），所以我们可以接下去按情形4、情形5或情形6来处理。
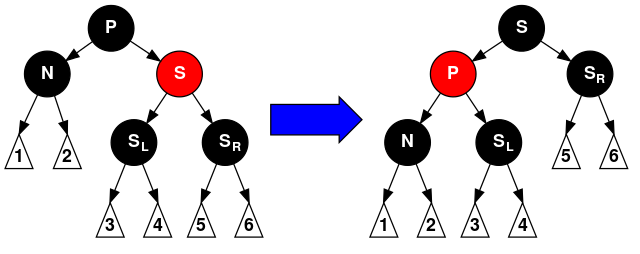
情形3: N的父亲、S和S的儿子都是黑色的。在这种情形下，我们简单的重绘S为红色。结果是通过S的所有路径，它们就是以前不通过N的那些路径，都少了一个黑色节点。因为删除N的初始的父亲使通过N的所有路径少了一个黑色节点，这使事情都平衡了起来。但是，通过P的所有路径现在比不通过P的路径少了一个黑色节点，所以仍然违反性质5。要修正这个问题，我们要从头开始，在P上做重新平衡处理。
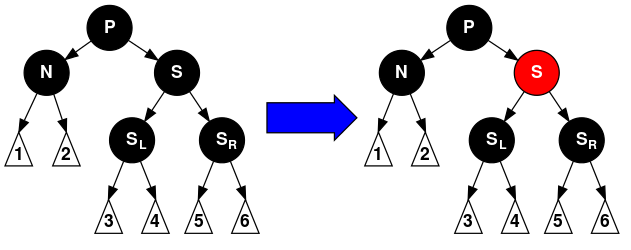
情形4: S和S的儿子都是黑色，但是N的父亲是红色。在这种情形下，我们简单的交换N的兄弟和父亲的颜色。这不影响不通过N的路径的黑色节点的数目，但是它在通过N的路径上对黑色节点数目增加了一，添补了在这些路径上删除的黑色节点。
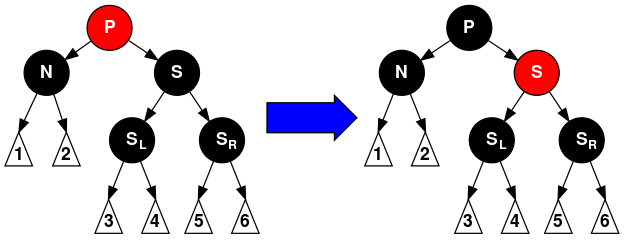
情形5: S是黑色，S的左儿子是红色，S的右儿子是黑色，而N是它父亲的左儿子。在这种情形下我们在S上做右旋转，这样S的左儿子成为S的父亲和N的新兄弟。我们接着交换S和它的新父亲的颜色。所有路径仍有同样数目的黑色节点，但是现在N有了一个右儿子是红色的黑色兄弟，所以我们进入了情形6。N和它的父亲都不受这个变换的影响。
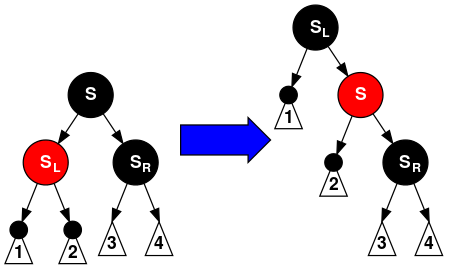
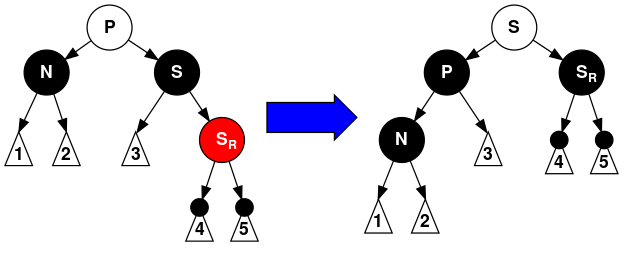
情形6：S是黑色，S的右儿子是红色，而N是它父亲的左儿子。在这种情形下我们在N的父亲上做左旋转，这样S成为N的父亲（P）和S的右儿子的父亲。我们接着交换N的父亲和S的颜色，并使S的右儿子为黑色。子树在它的根上的仍是同样的颜色，所以性质3没有被违反。但是，N现在增加了一个黑色祖先: 要么N的父亲变成黑色，要么它是黑色而S被增加为一个黑色祖父。所以，通过N的路径都增加了一个黑色节点。在示意图中的白色节点可以是红色或黑色，但是在变换前后都必须指定相同的颜色。

AVL tree和Red-Black tree比较

两者支持的操作相同，且基本操作的时间复杂度都是 $O(logn)$ 。
对于查找操作比较多的应用，AVL tree比red-black tree快一点，因为它更严格平衡。而插入和删除操作，AVL tree就相应会慢一点。

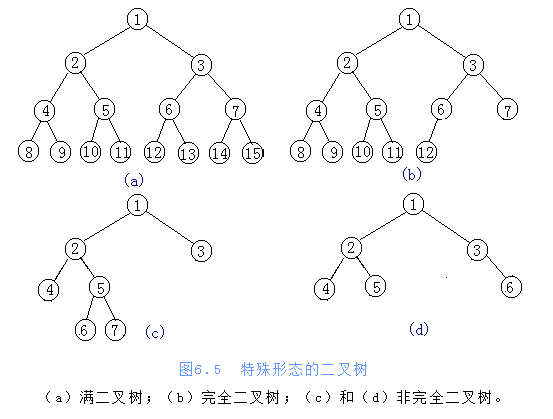
满二叉树(Full Binary Tree)

一棵深度为k且具有 $2^k-1$ 个节点的二叉树称为满二叉树。

每一层上的节点数都是最大节点树。

完全二叉树(Complete Binary Tree)

深度为k的，有n个节点的二叉树，当且仅当其每个节点都与深度为k的满二叉树中从上而下从左至右的编号从1至n的节点一一对应时，称为完全二叉树。
完全二叉树除最后一层之外全是满的，最后一层所有的结点都在最左侧。

具有n个节点的完全二叉树的深度为 $log_2n+1$ 。
如果对一棵有n个节点的完全二叉树的节点按层序编号（从第1层到第 $log_2n+1$ 层，每层从左到右），则对任一节点i( $1 \leqslant i \leqslant n$ )，有：

(1) 如果i=1，则节点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是节点i/2。
(2) 如果2i>n，则节点i无左孩子(节点i为叶子节点)；否则其左孩子LCHILD(i)是节点2i。
(3) 如果2i+1>n，则节点i无右孩子；否则其右孩子RCHILD(i)是节点2i+1。

满二叉树与完全二叉树

一些特殊树

字典树(Trie)

字典树又称前缀树，是一种有序树，用于保存关联数组，其中的键通常是字符串。
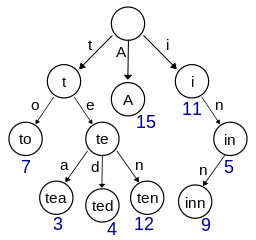
一个保存了8个键的trie结构，"A","to","tea","ted","ten","i","in","inn"。键标注在节点中，值标注在节点之下。每一个完整的英文单词对应一个特定的整数。键不需要被显式地保存在节点中。图中标注出完整的单词，只是为了演示trie的原理。

与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。
一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，也就是这个节点对应的字符串，根节点对应空字符串。
一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。
trie树常用于搜索提示。如，当输入一个网址时，自动搜索可能的选择。当没有完全匹配的搜索结果，返回前缀最相似的可能。

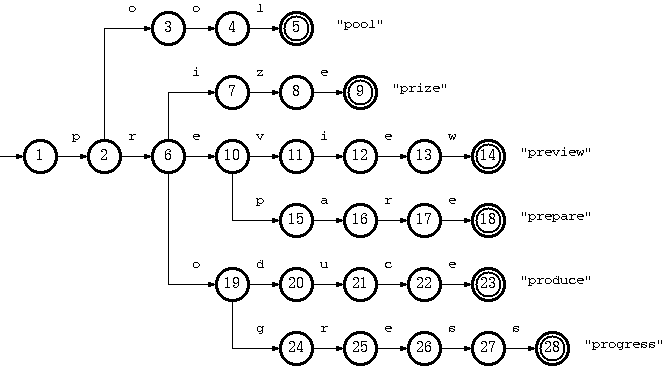
另一个Trie的例子

trie也可以视为一个确定优先状态机(deterministic finite automation)。每个节点视为一个状态，每一个边视为一个转换。
DFA常常用转换表(trainsition table)实现。横行是状态，竖列是转换标记。每个空间存储的是经过这个转换，下一步要到达的状态。
这种方式在空间存储上是不划算的，trie树中的节点只有几个分支，表中的大部分空间都会是空的。
trie的实现进行了改良。有两种方式Double-Array Trie、Tripple-Array Trie。

二数组字典树

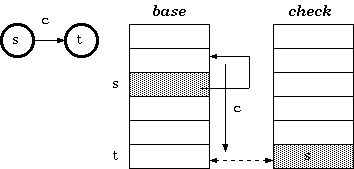
Double-Array Trie Data Structure
数据结构包含2个数组：base/check。

base存储的是trie的节点。
check数组表示某个节点的前驱节点。

定义：对于一个把c作为输入，从s到t的转换，二数组字典树中的实现是：
check[base[s]+c] = s
base[s] + c = t

三数组字典树

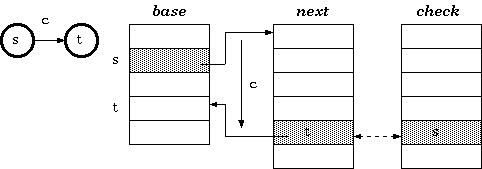
Tripple-Array Trie Data Structure
数据结构包含3个数组：base/next/check。

base存储的是trie的节点。
next存储的是base中的节点经过转换后的节点。
check用于检查，表示某个节点的前驱节点。

定义：对于一个把c作为输入，从s到t的转换，三数组字典树中的实现是：
check[base[s]+c] = s
next[base[s]+c] = t

哈夫曼树(Huffman Tree)

哈夫曼树又称最优树，基本思想是使权大的节点靠近根，从而使编码总长度最小。
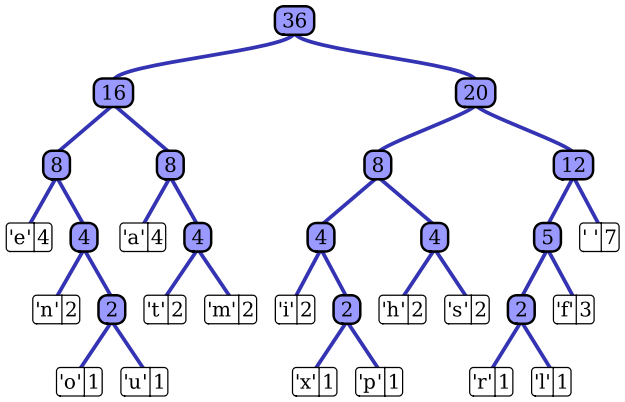
按照"this is an example of a huffman tree"中的字母频率构造的哈夫曼树
对应表格：

字符	空格	a	e	f	h	i	m	n	s	t	l	o	p	r	u	x
频率	7	4	4	3	2	2	2	2	2	2	1	1	1	1	1	1
编码	111	010	000	1101	1010	1000	0111	0010	1011	0110	11001	00110	10011	11000	00111	10010

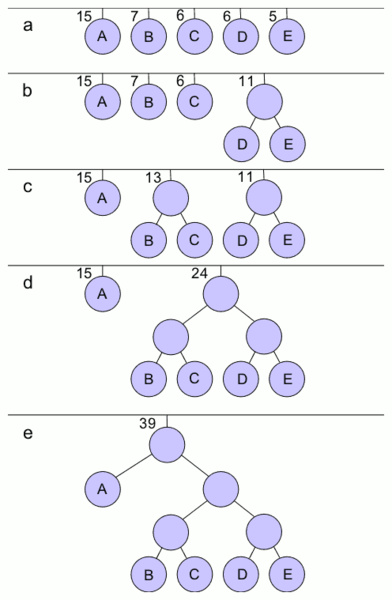
第一步：初始化n个单节点的树，并为它们标上字母表中的字符。把每个字符的概率记在树的根中，用来指出树的权重(更一般地说，树的权重等于树中所有叶子的概率之和)。
第二步：重复下面的步骤，直到只剩一棵单独的树。找到两棵权重最小的树(次序无关紧要)。把它们作为新树中的左右子树，并把其权重之和作为新的权重记录在新树的根中。

操作要点是对权值的合并、删除与替换，总是合并当前值最小的两个。

哈夫曼编码演算步骤

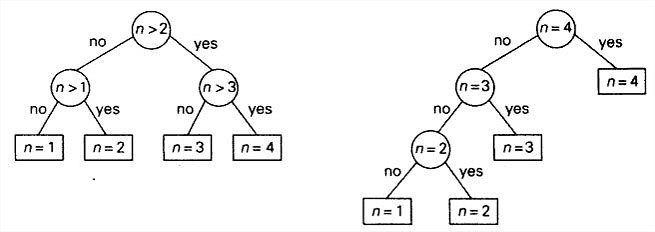
哈夫曼算法也可用于数字都在叶节点上的最优决策树构造。比如下图，因为n为1234的概率不同，生成的最优决策树也不同。左图中，n为1234的概率p均为0.25。右图中，p1=0.1,p2=0.2,p3=0.3,p4=0.4。
猜测1~4之间整数，在不同概率下的两棵最优决策树

堆

堆总是一棵完全二叉树。其中(最大堆)任意节点都大于它的后裔，最大元在堆的根上。
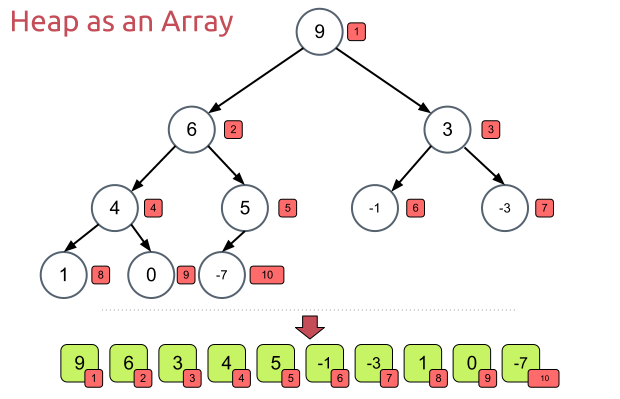
最大堆的数组表示
关于堆的详细讲解看这里。