概率与统计直觉

整理 cs229 与微软在 Edx 上课程 Data Science Orientation 的笔记，深度学习花书第3章，还有概率导论里的一些内容。

cs229 - Review of Probability Theory

概率论重要知识点。

目录

1. Elements of probability
   a. Conditional probability and independence
2. Random variables
   a. Cumulative distribution functions
   b. Probability mass functions
   c. Probability density functions
   d. Expectation
   e. Variance
   f. Some common random variables
3. Two random variables
   a. Joint and marginal distributions
   b. Joint and marginal probability mass functions
   c. Joint and marginal probability density functions
   d. Conditional distributions
   e. Bayes’s rule
   f. Independence
   g. Expectation and covariance
4. Multiple random variables
   a. Basic properties
   b. Random vectors
   c. The multivariate Gaussian distribution

文件

Review of Probability Theory

Microsoft - Statistical Insights

统计学相关知识点。

目录

1. What is a Variable?
   Why is this important?
2. Population vs. Sample
   Why is this important?
3. Measures of Central Tendency
4. Measures of Variability
   Why is this important?
5. Hypothesis Testing
   Why Don’t We “Accept” the Null Hypothesis?
6. Measures of Association: Correlation Coefficients
   How to Interpret a Correlation Coefficient
   How to Calculate a Correlation Coefficient
   Rules of Thumb for Correlations
7. Comparative Measures: One Sample t-Test
   How to Calculate a One Sample t-Test Statistic
8. Comparative Measures: Two Sample t-Test
   How to Calculate a Two Sample t-Test Statistic
9. Comparative Measures: Paired Sample t-Test
   How to Calculate a Paired Sample t-Test Statistic
10. Comparative Measures: Analysis of Variance (ANOVA)
    Why You Shouldn’t Run Multiple t-Tests
    How to Calculate a One-Way ANOVA
    How to Calculate a Two-Way ANOVA
11. Predictive Measures: Linear Regression
    How to Calculate a Regression

文件

Statistical Insights

深度学习 - 第3章 概率与信息论

针对深度学习中所需要的概率论。

为什么要使用概率

因为机器学习通常必须处理不确定量，有时也可能需要处理随机(非确定性的)量。
不确定性有3种可能的来源：

• 被建模系统内在的随机性。
• 不完全观测。
• 不完全建模。

概率直接与事件发生的频率相联系，是频率派概率；涉及确定性水平，是贝叶斯概率。

随机变量、概率分布、边缘概率、条件概率、条件概率的链式法则、独立性和条件独立性 、期望方差和协方差

一个随机变量只是对可能的状态的描述，它必须伴随着一个概率分布来指定每个状态的可能性。
协方差在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度。协方差矩阵的对角元是方差。

常用概率分布

当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎样的形式时，正态分布是默认的比较好的选择。有两个原因：

• 我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理说明很多独立随机变量和近似服从正态分布。这意味着在实际中，很多复杂系统都可以被成功地建模成正态分布的噪声，即使系统可以被分解成一些更结构化的部分。
• 在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。因此，我们可以认为正态分布是对模型加入的先验知识量最少的分布。

高斯混合模型是概率密度的万能近似器，任何平滑的概率密度都可以用具有足够多组件的高斯混合模型以任意精度来逼近。

常用函数的有用性质、贝叶斯规则

logistic sigmoid

$\sigma(x) = \frac{1}{1 + exp(-x)}$

通常用来产生 Bernouilli 分布中的参数 $\phi$，因为其值域是(0,1)，在其有效取值范围内。

softplus

$\zeta(x) = log(1 + exp(x))$

用来产生正态分布的 $\beta$ 和 $\alpha$参数，因为它的范围是$(0, \infty)$。

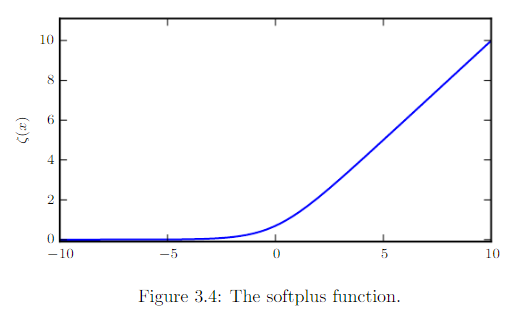
一些有用的性质

信息论

信息论是应用数学的一个分支，主要研究的是对一个信号包含信息的多少进行量化。本书主要是用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。
信息论的基本想法是一个不太可能的事件居然发生了，要比一个非常可能的事件发生，能提供更多的信息。

一个事件$x = x$的自信息 self-information 为：

$I(x) = -\log P(x)$

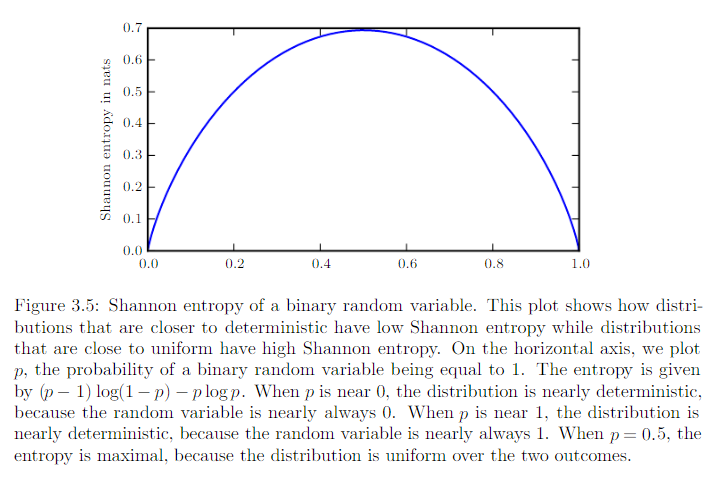
香农熵 Snannkon entropy

对整个概率分布中的不确定性总量进行量化。是指遵循这个分布的时间所产生的期望信息总量。

$H(x) = E_{\sim P}[I(x)] = -E_{x \sim P}[log P(x)]$

接近确定性的分布 (输出几乎可以确定) 具有较低的熵，接近均匀分布的概率分布有较高的熵。

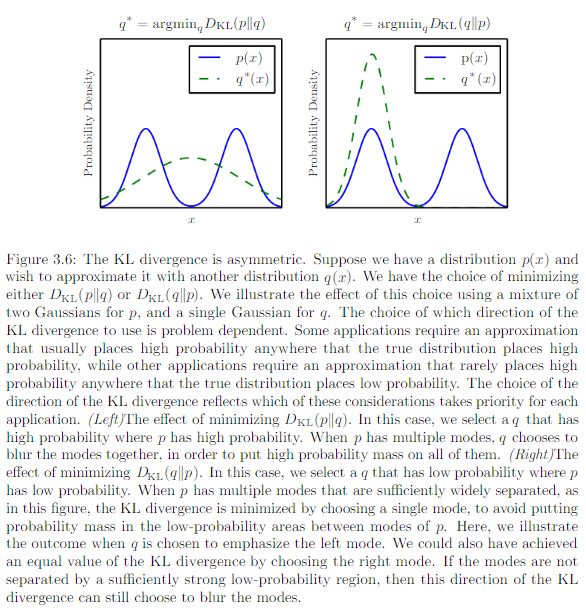
KL 散度 Kullback-Leibler (KL) divergence

对于同一个随机变量 $x$ 有两个单独的概率分布 $P(X)$ 和 $Q(x)$，可以使用 KL 散度来衡量这两个分布的差异。

$D_{KL}(P \parallel Q) = E_{x \sim P} [\log \frac{P(x)}{Q(x)}] = E_{x \sim P} [\log P(x) - \log Q(x)]$

在离散型变量情况下，KL 散度衡量的是，当我们使用一种被设计成能够使得概率分布 $Q$ 产生的消息的长度最小的编码，发送包含由概率分布 $P$ 产生的符号的消息时，所需要的额外信息量。

KL 散度的性质：
非负。如果为0，当且仅当 P 和 Q 在离散型变量的情况下是相同的分布，或者在连续性变量的情况下是几乎处处相同的。
KL 散度是不对称的。

交叉熵 cross-entropy

与 KL 散度很像。针对 Q 最小化交叉熵等价于最小化 KL 散度。todo

$H(P,Q) = H(P) + D_{KL}(P \parallel Q)$

$H(P,Q) = - E_{x \sim P} \log Q(x)$

结构化概率模型

用图表示概率分布的分解。只是概率分布的一种特殊描述。
有向或无向，图的每个节点对应这一个随机变量，连接两个随机变量的边意味着概率分布可以表示为这两个随机变量之间的直接作用。
有向：

$p(x) = \prod_i p(x_i | P_{aG}(x_i))$

无向：

$p(x) = \frac{1}{Z} \prod_i \phi^{(i)} (C^{(i)})$

概率导论

doing

Ref:
[1] cs229
[2] Edx - Microsoft Professional Program Certificate in Data Science = Data Sciencae Orientation
[3] 概率导论