Boosting
工作机制:
先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注 (re-weighting 或 re-sampling),然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值 T,最终将这 T 个基学习器进行加权结合。
注意,Boosting 算法在训练的每一轮都要检查当前生成的基分类器是否满足基本条件,一旦条件不满足,则当前基学习器即被抛弃,且学习过程停止。
从偏差-方差的角度看,Boosting 主要关注降低偏差,因此 Boosting 能基于泛化性能相当弱的学习器构建出很强的集成。
这里面有两个问题需要回答:
- 在每一轮学习之前,如何改变训练数据的权值分布?
- 如何将一组弱分类器组合成一个强分类器?
具体不同的boosting实现,主要区别在弱学习算法本身和上面两个问题的回答上。
Main boosting types
- Weight based.
- Residual based.
Weight Based Boosting
Weight based boosting parameters
- Learning rate (or shrinkage or eta)
- Number of estimators
- Input model - can be anything that accepts weights
- Sub boosting type:
- AdaBoost - Good implementation in sklearn (python)
- LogitBoost = Good implementation in Weka (Java)
AdaBoost
两个问题的回答:
- 提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。
- 加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用;减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。


解释


另一个解释
AdaBoost 算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。
前向分步算法
加法中的每一步都最小化当前步损失函数。

算法:

前向分步算法与 AdaBoost
AdaBoost 算法是前向分步算法的特例。这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。
Residual Based Boosting
Residual Based Boosting Parameters
- Learning rate (or shrinkage or eta)
- Number of estimators
- Row (sub) sampling
- Column (sub) sampling
- Input model - better be trees.
- Sub boosting type:
- Fully gradient based.
- Dart
Residual Based Favourite Implementations
- Xgboost
- Lightgbm
- H2O’s GBM
- Catboost
- Sklearn’s GBM
Boosting Tree 提升树
Boosting Tree:采用加法模型(即基函数的线性组合)与前向分步算法,以决策树为基函数的提升方法。初始树对训练数据拟合,后续树拟合残差。
上文提到的基本分类器 x<v 或 x>v 可以看作是由一个根节点直接连两个叶节点的决策树桩 decision stump。
提升树模型可以表示为决策树的加法模型:

提升树算法
不同问题的提升树学习算法,主要区别在于使用的损失函数不同:
- 回归问题:用平方误差损失函数。
- 分类问题:用指数损失函数。
- 决策问题:用一般损失函数。

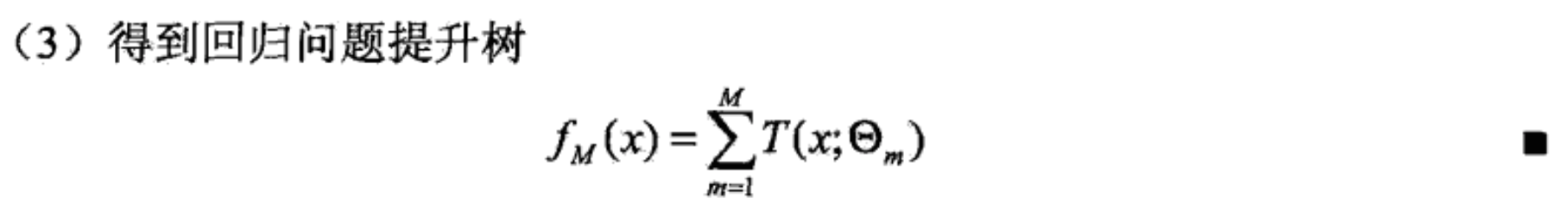
梯度提升
Ref
[1] 统计学习方法
[2] 机器学习 - 周志华
[3] Coursera - How to Win a Data Competition