Cluster 聚类

无监督学习 unsupervised learning。

聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个簇 cluster。

聚类既能作为一个单独过程，用于找寻数据内在的分布结构，也可作为分类等其他学习任务的前驱过程。比如，商业中对新用户的类型先聚类，然后基于这些类训练分类模型，用于判断新用户的类型。也可用于异常检测，远离簇中心的样本为异常点，或密度极低处的样本为异常点。

聚类算法设计的两个基本问题：性能度量、距离计算。

性能度量

聚类结果的簇内相似度 intra-cluster similarity 高，且簇间相似度 inter-cluster similarity 低。

两类：

• 将聚类结果与某个参考模型 reference model 进行比较，称为外部指标 external index。
• 直接考察聚类结果而不利用任何参考模型，称为内部指标 internal index。

外部指标：

内部指标：

距离计算

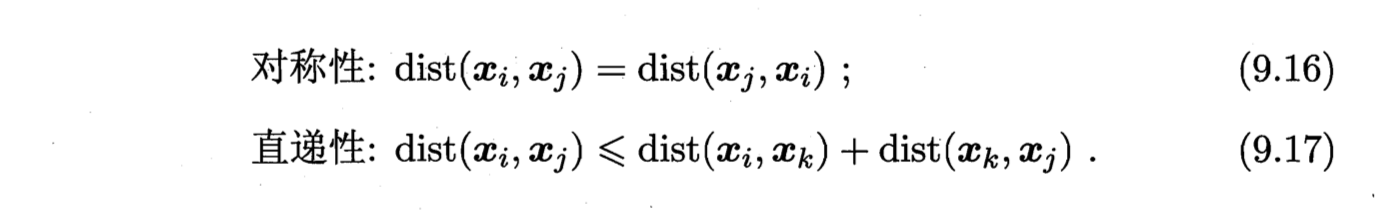
对于有序属性 ordinal attribute，可用闵可夫斯基距离。

对于无序属性 non-ordinal attribute，可用 VDM (Value Difference Metric)。
比较各自在总数里的比例。

可以将两者结合起来处理混合属性。

注意：如果我们只是基于某种形式的距离来定义”相似度度量 similarity measure”，距离越大，相似度越小，就不必要满足所有性质尤其是直递性。此时距离称为”非度量距离 non-metric distance”。

prototype-based clustering 原型聚类

prototype-based clustering，此类算法假设聚类结构能通过一组原型刻画。
通常情况下，算法先对原型进行初始化，然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式，将产生不同的算法。

k-means k 均值算法

k-means k 均值算法

Learning Vector Quantization 学习向量量化

与一般聚类算法不同的是，LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
首先初始化 q 个原型向量 center，然后开始迭代。每轮迭代，算法随机选取一个有标记训练样本，找出与其距离最近的原型向量，并根据两者的类别标记是否一致来对原型向量进行相应的更新，靠近一点或是远离一点。直到更新量很小或到达最大迭代轮数。

Mixture-of-Gaussian 高斯混合聚类

采用概率模型来表达聚类原型。假设样本由几个高斯分布给出，簇划分由原型对应后验概率确定，极大似然估计，EM 算法求解。

将高斯分布的概率密度函数记为$p(x|\mu, \Sigma)$。

假设样本的生成过程由高斯混合分布给出。首先$\alpha$是每个子高斯分布的概率，然后每个子的按照各自的分布采样。

因此，从原型聚类的角度来看，高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画，簇划分则由原型对应后验概率确定。

density-based clustering 密度聚类

此类算法假设聚类结果能通过样本分布的紧密程度确定。通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇已获得最终的聚类结果。

DBSCAN

簇是密度可达关系导出的最大的密度相连样本集合。先找到所有核心对象(周围有很多点密度直达)，然后从任一核心对象触发，找到其密度可达的样本生成聚类簇，直到所有核心对象均被访问过。

概念定义：



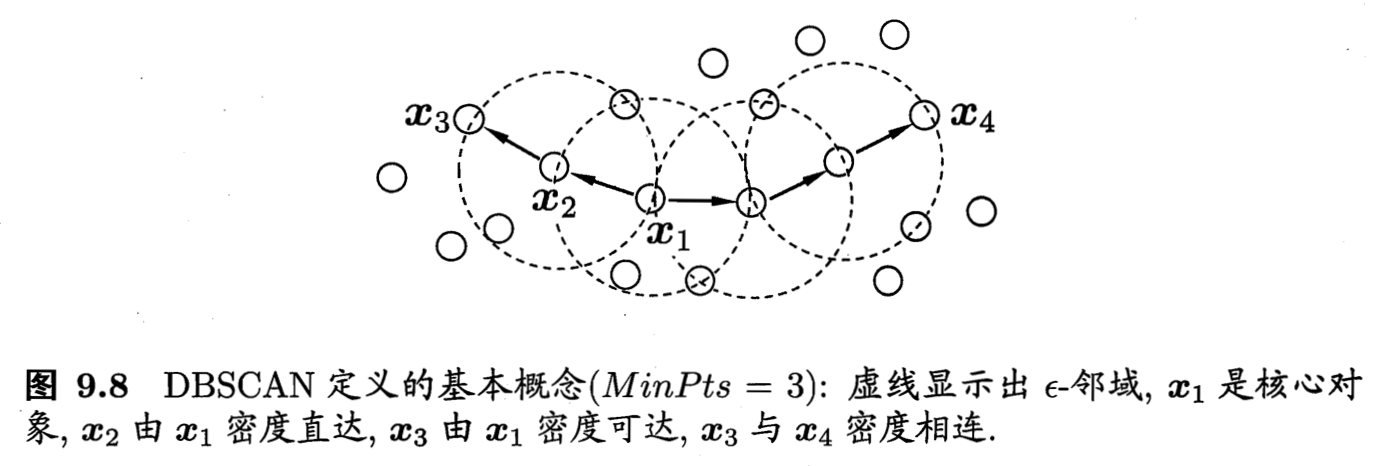
定义簇：

算法：
先找出所有的核心对象。然后以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。

hierarchical clustering 层次聚类

层次聚类试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用自底向上的聚合策略，也可采用自顶向下的分拆策略。

AGNES

自底向上聚合策略。
先将数据集中的每个样本看做一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。
这里的关键是如何计算聚类簇之间的距离。也即集合的某种距离。

最小距离由两个簇的最近样本决定；最大距离由两个簇的最远样本决定；平均距离由两个簇的所有样本共同决定。分别这三种时，AGNES 算法被相应地称为 single-linkage 单链接、complete-linkage 全链接、average-linkage 均链接。


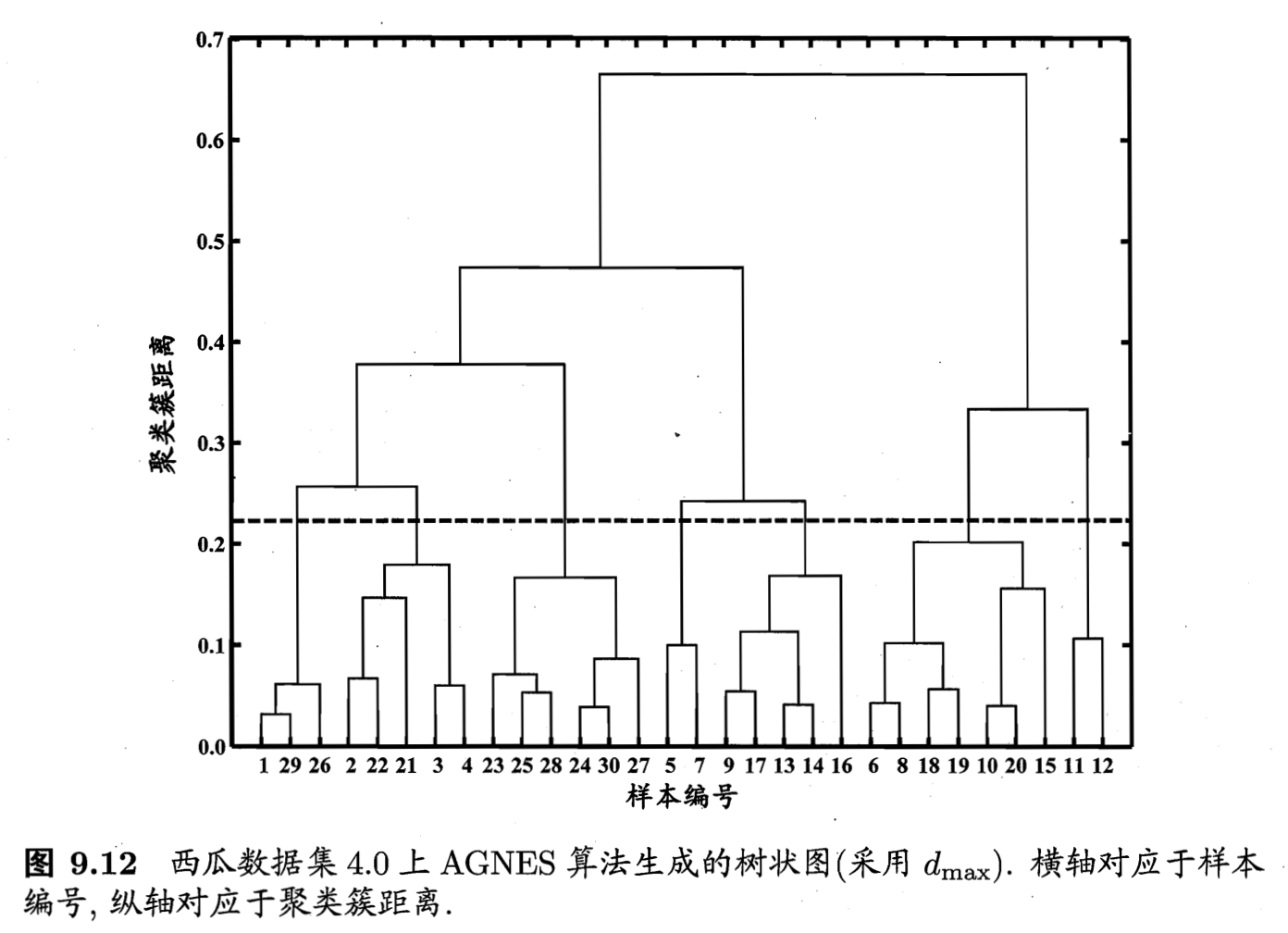
从分割层逐步提升，可得到聚类簇逐渐减少的聚类结果。

Ref

[1] 机器学习 - 周志华