降维与度量学习

k Nearest Neighbour k 近邻学习

k Nearest Neighbour k 近邻学习

低维嵌入

KNN 算法中的讨论基于一个重要假设：任意测试样本$x$附近任意小的$\delta$距离范围内总能找到一个训练样本，即训练样本的采样密度足够大，或称为密采样 dense sample。然而这个假设在现实任务中通常很难满足。
维数灾难 curse of dimensionality：高维情形下出现的数据样本稀疏、距离计算困难。
解决方法：降维 dimension reduction，因为数据样本虽然是高维的，与学习任务密切相关的也许仅是某个低维分布，即高维空间中的一个低维嵌入 embedding。

Multiple Dimensional Scaling 算法 ? todo

线性变换

对原始高维空间进行线性变换以获得低维子空间。

对降维效果的评估，通常是比较降维前后学习器的性能。如果维数降至二维或三维，则可通过可视化技术来直观地判断降维效果。

Principle Component Analysis 主成分分析

Principle Component Analysis 主成分分析

核化线性降维

线性降维方法假设从高维空间到低维空间的函数映射是线性的。但现实问题中有时需要非线性映射才能找到恰当的低维嵌入。

非线性降维的一种常用方法，是基于 kernel trick 对线性降维方法进行核化 kernelized。

Kernelized PCA 核主成分分析

原始点到转换后的原始点的映射为$\phi$，即$z_i = \phi (x_i)$。恰好 PCA 的欲求解问题里有个內积。

manifold learning 流形学习

效果通常一般，因为有效进行邻域保持需要密采样，恰是高维情形下的重大障碍。

Isometric Mapping 等度量映射

保持近邻样本之间的距离。
低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，因为高维空间中的直线距离在低维嵌入流形上是不可达的。

那么实际的测地线距离如何测算？利用流形在局部上与欧氏空间同胚的性质，对每个点基于欧氏距离找出其近邻点，然后就能建立一个近邻连接图，图中近邻点之间存在连接，而非近邻点之间不存在连接。计算两点之间测地线的问题就变成计算邻近连接图上两点之间的最短路径问题。Dijkstra 或 Floyd 算法计算最短路径，得到任意两点距离之后，就可用 MDS 方法获得样本在低维空间中的坐标。

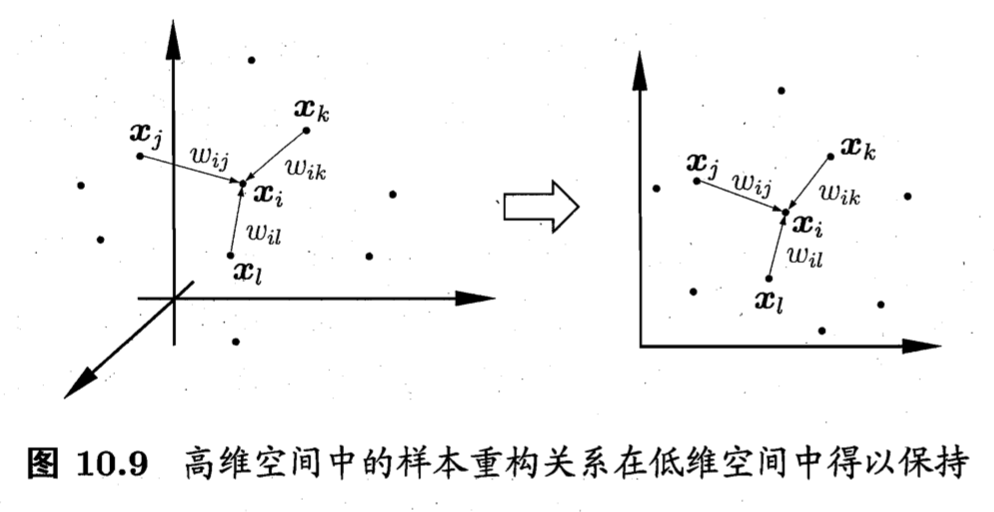
Locally Linear Embedding 局部线性嵌入

保持邻域内样本之间的线性关系。

Metric Learning 度量学习

降维的主要目的是找到一个合适的低维空间，在此空间中进行学习能比原始空间性能更好。事实上，每个空间对应了在样本属性上定义的一个距离度量。那可以直接尝试学习出一个合适的距离度量，这就是度量学习的基本动机。
马氏距离

对 M 进行学习需要一个目标。例如提高近邻分类器的性能，将 M 嵌入其评价指标进行学习。

Ref

[1] 机器学习 - 周志华