k Nearest Neighbour k 近邻学习

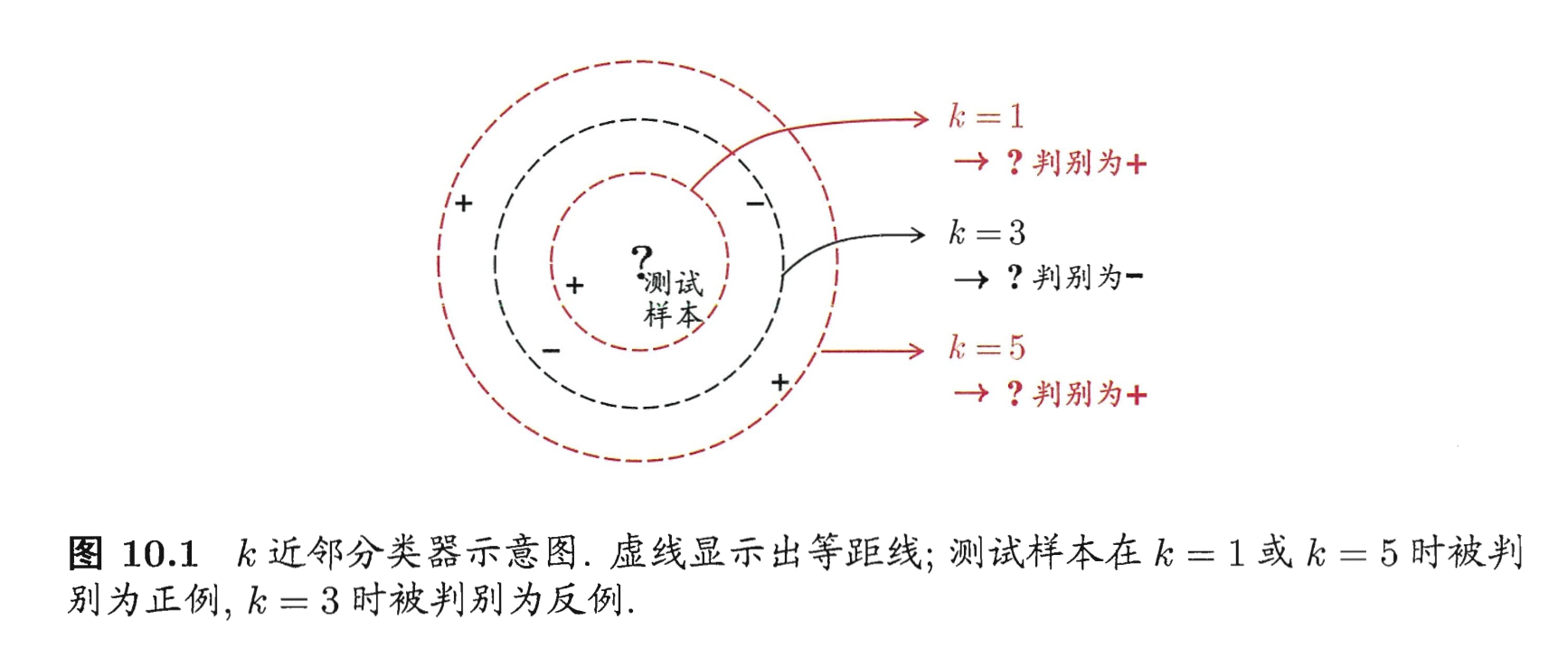
k-Nearest Neighbor：给定测试样本，基于某种距离度量找出训练集中与其最靠近的 k 个训练样本，然后基于这 k 个邻居的信息来进行预测。
lazy learning，没有显式的训练过程。训练阶段只是把样本保存起来，训练时间开销为0。(训练阶段就对样本就对样本进行学习处理的方法，称为 eager learning。)
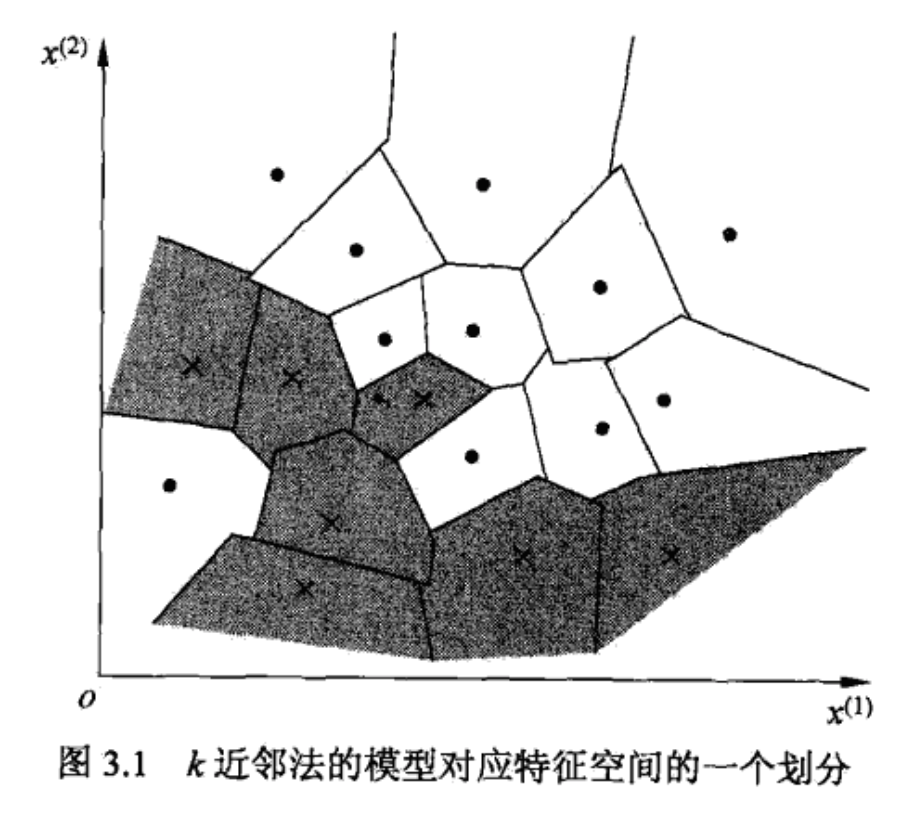
k 近邻法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的模型。
三个基本要素：k 值的选择、距离度量、分类决策规则。

模型

距离度量

特征空间中两个实例点的距离是两个实例点相似程度的反映。
常见的几种距离：


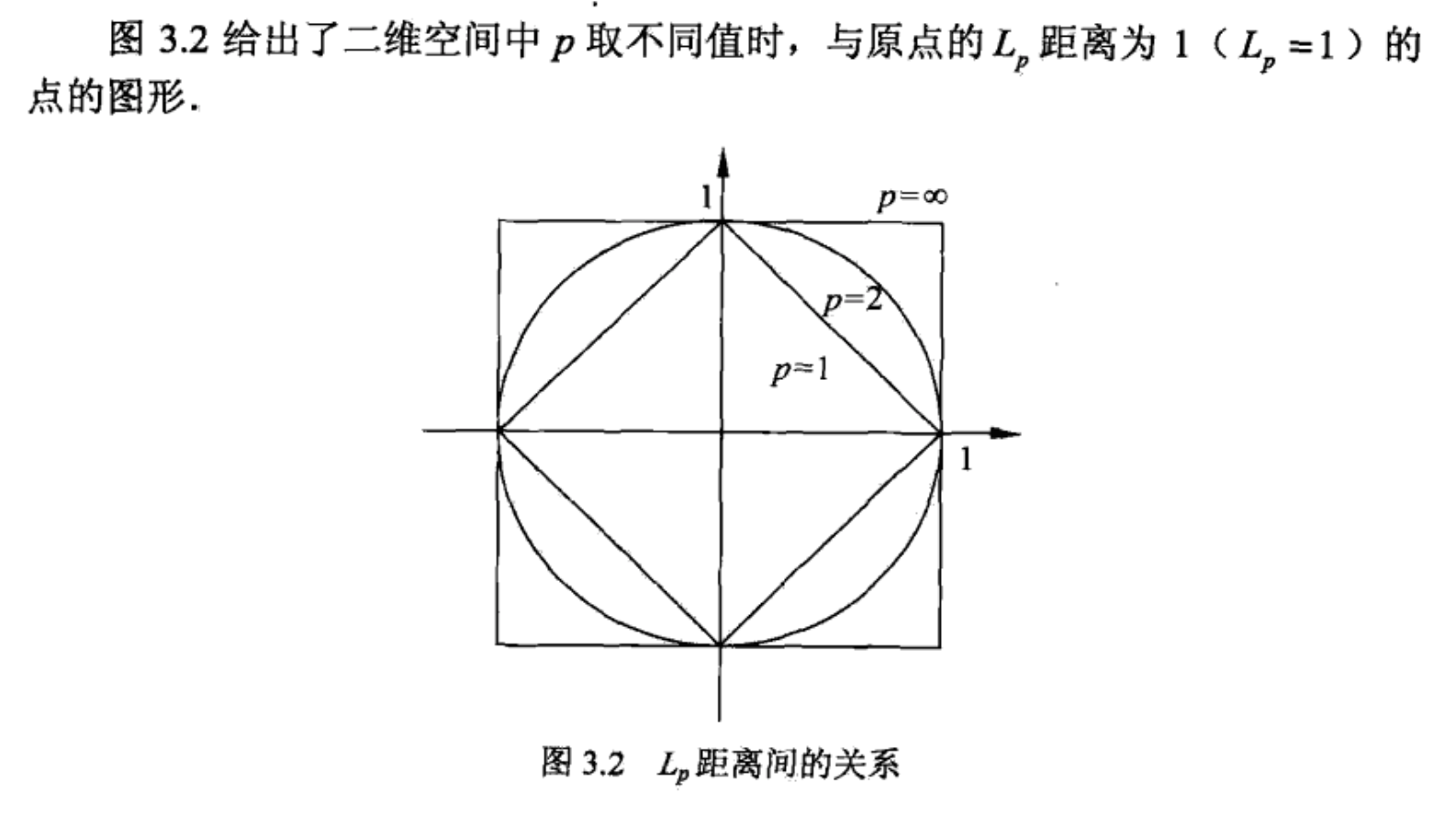
由不同的距离度量所确定的最近邻点是不同的。

k 值的选择

k 值的选择会对 k 近邻法的结果产生重大影响。
k 值较小：只用较小邻域的训练实例。近似误差 approximation error 会小，估计误差 estimation error 会大，预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。k 值的减少就意味着整体模型变得复杂，容易发生过拟合。
k 值较大：使用较大邻域的训练实例。估计误差小，近似误差大。遥远的训练实例也有话语权。k 值的增大意味着整体的模型变得简单。
应用中，k 值一般取一个比较小的数值，通常采用交叉验证法来选取最优的 k 值。

分类决策规则

往往是多数表决。

分类任务中使用(加权)投票法。回归任务中使用(加权)平均法。

评估准确率

问题假设：k = 1，二分类

k 近邻法的实现：kd 树

实现主要要考虑：如何对训练数据进行快速 k 近邻搜索。当特征空间维度大或者训练数据容量大的时候尤为重要。
线性扫描不可取，太慢。可以考虑使用特殊的结构存储，以减少计算距离的次数。

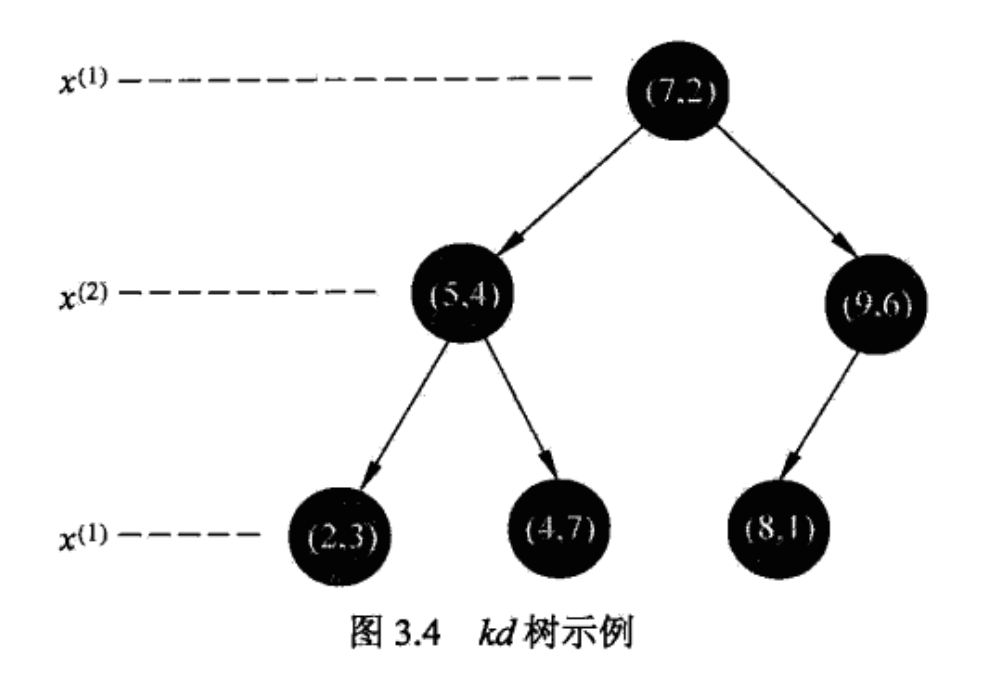
构造 kd 树

根据规则选择某个维的中位数生成一个节点切分子区域，直到子区域为空，每个节点只有一个数据时为止。
kd 树是一种对 k 维空间中的实例点进行存储以便对其快速检索的树形数据结构。kd 树是二叉树，表示对 k 维空间的一个划分 partitioin。构造 kd 树相当于不断地用垂直于坐标轴的超平面将 k 维空间划分，构成一系列的 k 维超矩形区域。这里 k 的含义和 k 临近里的 k 意义不同。
每个节点都是一个样本，切分在中位数。

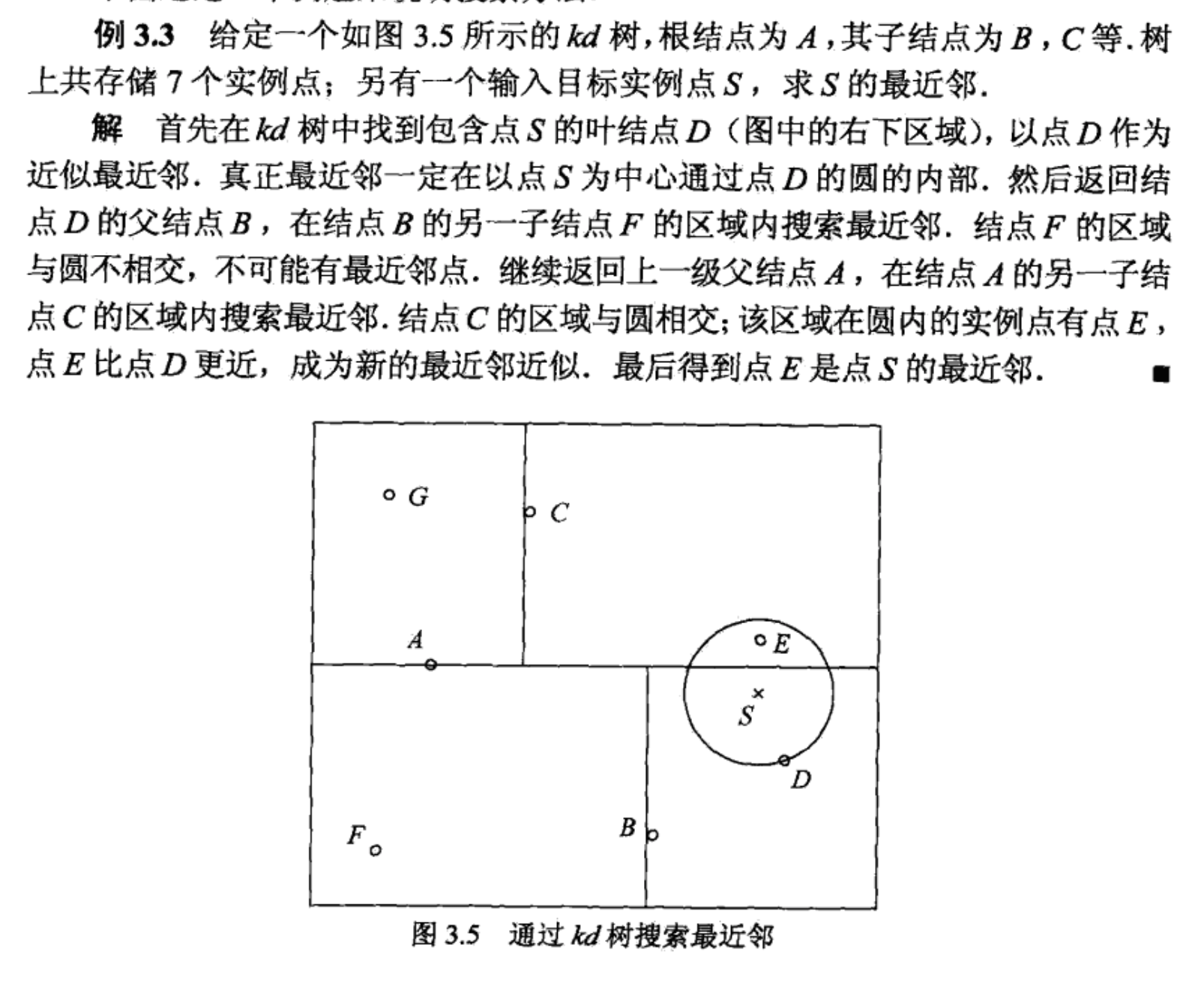
搜索 kd 树

搜索 k 近邻时，首先找到包含目标点的叶节点；然后从该叶节点出发，依次回退到父节点；不断查找与目标点最邻近的节点，当确定不可能存在更近的节点时终止。这样搜索就被限制在空间的局部区域上，效率大为提高。


如果实例点是随机分布的，kd 树搜索的平均时间复杂度是 O(logN)，N 是训练实例数。kd 树更适于训练实例数远大于空间维数时的 k 近邻搜索。空间维数接近训练实例数时，会接近线性扫描。

库

scikit-learn

Ref

[1] 机器学习 - 周志华
[2] 统计学习方法
[3] Coursera - How to Win a Data Science Competition