Bayesian 贝叶斯分类器

A Stellar Hiker

2018-03-30

Machine Learning

概述

为避免贝叶斯定理求解时面临的组合爆炸、样本稀疏问题，朴素贝叶斯分类器引入了属性条件独立性假设。这个假设在现实中往往很难成立。但朴素贝叶斯分类器却常常效果很好。

根据对属性间依赖的涉及程度：

朴素贝叶斯分类器：不考虑属性间依赖性。
半朴素贝叶斯分类器
贝叶斯网：表示任意属性间的依赖性。

贝叶斯分类器：通过最大后验概率进行单点估计。贝叶斯学习：进行分布估计。

贝叶斯决策论

极大似然估计

Naive Bayes Classifier 朴素贝叶斯分类器

基于贝叶斯公式 $P(c|x) = \frac{P(c)P(x|c)}{P(x)}$ 来估计后验概率 $P(c|x)$ 的主要困难是：类条件概率 $P(x|c)$ 是所有属性上的联合概率，难以从有限的训练样本直接估计而得。(基于有限训练样本直接估计联合概率，在计算上将会遭遇组合爆炸问题，在数据上将会遭遇样本稀疏问题；属性数越多，问题越严重。)
朴素贝叶斯采用了属性条件独立性假设 attribute conditional independence assumption：对已知类别，假设所有属性相互独立。

Image Loading

学习与分类算法

Naive Bayes Classifier 的训练过程就是基于训练集 D 来估计类先验概率 $P(c)$ ，并为每个属性估计条件概率 $P(x_i|c)$ 。
Image Loading

贝叶斯估计 - 拉普拉斯修正 Laplacian correction

用极大似然估计可能会出现所要估计的概率值为0的问题。例如，某个属性值在训练集中没有与某个类同时出现过。
Image Loading

注意，拉普拉斯修正实际上假设了属性值与类别均匀分布，这是在朴素贝叶斯学习过程中额外引入的关于数据的先验。

现实任务中朴素贝叶斯分类器有多种使用方式。例如：

若任务对预测速度要求较高，则对给定训练集，可将朴素贝叶斯分类器设计的所有概率估值实现计算好存储起来，这样在进行预测时只需查表即可进行判别。
若任务数据更替频繁，则可采用 lazy learing，先不进行任何训练，待收到预测请求时再根据当前数据集进行概率估值；
若数据不断增加，则可在现有估值基础上，仅对新增样本的属性值所涉及的概率估值进行计数修正即可实现增量学习。

Semi-Naive Bayes Classifiers 半朴素贝叶斯分类器

朴素贝叶斯分类器采用了属性条件独立性假设，半朴素贝叶斯分类器 semi-naive Bayes classifiers 这类想要对这个假设进行一定程度的放松。
半朴素贝叶斯分类器的基本想法是，适当考虑一部分属性间的相互依赖信息，从而既不需进行完全联合概率计算，又不至于彻底忽略了比较强的属性依赖关系。
独依赖估计 One-Dependent Estimator，假设每个属性在类别之外最多仅依赖于一个其他属性，即：
Image Loading
问题的关键变为如何确定每个属性的父属性。

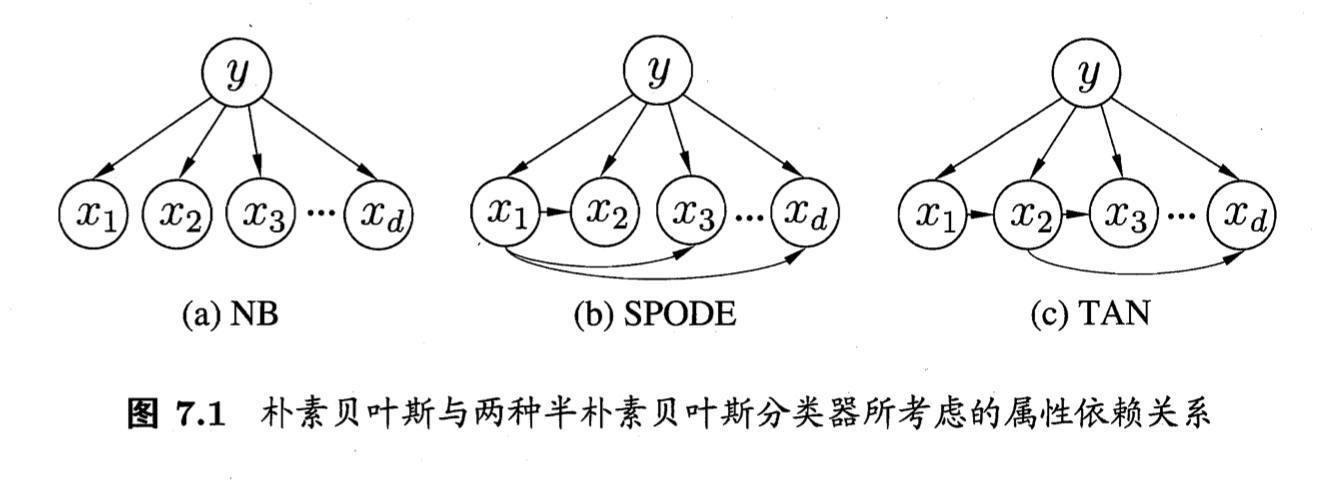
SPODE，Super-Parent ODE，都是同一个父亲。
TAN，Tree Augmented naive Bayes，最大带权生成树基础上按如下步骤生成：
AODE，Averaged One-Dependent Estimator，基于集成学习机制。每个属性都做超父试试，然后把满足标准的做集成。

Bayesian Network / Belief Network 贝叶斯网

EM 算法

Ref

[1] 机器学习 - 周志华
[2] 统计学习方法