Maximum Likelihood 极大似然估计

估计类条件概率 -> 假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。

概率模型的训练过程就是参数估计的过程。

• 频率学派：参数是未知的固定值，因此可通过优化似然函数等准则来确定参数值。
• 贝叶斯学派：参数是未观察到随机变量，本身也有分布。可假定参数服从一个先验分布，然后基于观测数据来计算后验分布。

极大似然估计(频率学派)是试图在$\theta_c$所有可能的取值中，找到一个能使数据出现的可能性最大的值。最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
之所以用 Log 是为了防止连乘操作造成的下溢。
缺点是估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。

例1：
设样本服从正态分布$N(\mu, \sigma^2)$，则似然函数为：

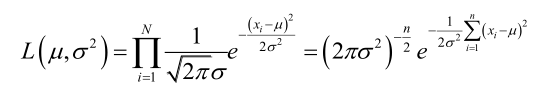
它的对数：

求导，得方程组：

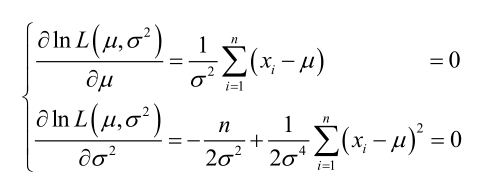
联合解得：

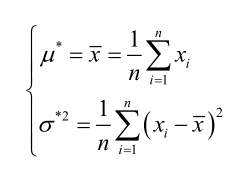
例2：
设样本服从均匀分布[a, b]。则X的概率密度函数：

对样本$D = \{x_1, x_2, \ldots, x_n\}$

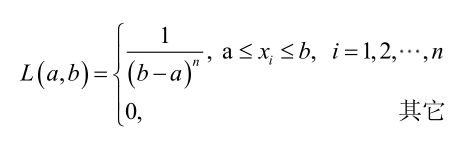
显然$L(a,b)$不连续，不能用导数来解。于是从极大似然估计的定义出发，求$L(a,b)$的最大值。
为使$L(a,b)$最大，$b-a$应该尽量小，但$b$不能小于$\max\{x_1, x_2, \ldots, x_n\}$，否则$L(a,b) = 0$。同理$a$不能大于$\min\{x_1, x_2, \ldots, x_n\}$。因此，$a$和$b$的极大似然估计：

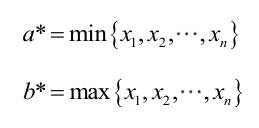
总结：
求最大似然估计量$\hat \theta$的一般步骤：

1. 写出似然函数；
2. 对似然函数取对数，并整理；
3. 求导数；
4. 解似然方程。

最大似然估计的特点：

1. 比其他估计方法更加简单；
2. 收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；
3. 如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计果。

Ref

[1] 统计学习方法
[2] 机器学习 - 周志华
[3] https://blog.csdn.net/zengxiantao1994/article/details/72787849