Decision Tree 决策树

决策树学习本质上是从训练数据集中归纳出一组分类规则。

基本流程

内部节点表示一个特征或属性，叶节点表示一个类。
决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。这样构建的树可能有过拟合现象，需要剪枝提高泛化能力。
决策树形成的决策边界是轴平行的 axis-parallel，好处是使学习结果有较好的可解释性，坏处是当真实分类边界比较复杂时，必须使用很多段划分才能获得较好的近似，复杂、耗时。

• 决策树可以看做一系列if-then规则。
• 决策树还看做给定特征条件下类的条件概率分布。X表示特征，Y表示类的随机变量，则这个条件概率分布可以表示为$P(Y|X)$。
  

决策树学习算法包含 特征选择、决策树生成、决策树剪枝 三部分。
决策树生成对应于模型的局部选择，只考虑局部最优；决策树剪枝对应于模型的全局选择，考虑全局最优。

特征选择

信息增益 - ID3

信息熵 information entropy。

信息增益 information gain，越大则纯度提高越多。

可选择增益最大的属性作为划分属性。
缺点：对可取值数据较多的属性有所偏好，可以理解为每个都撇成一个分支的话那一定每个分支内都最纯了。

增益率 - C4.5

增益率 gain ratio

缺点：对可取值数目较少的属性有偏好。
C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

基尼指数 - CART

基尼指数 Gini index

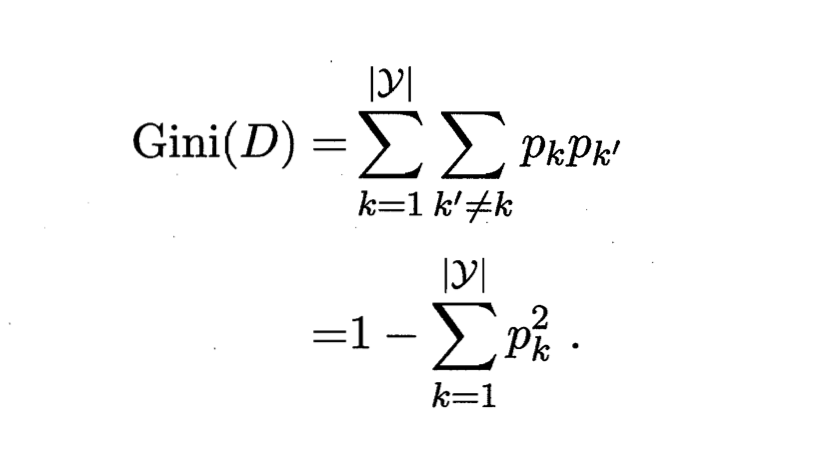
Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此Gini(D)越小，则数据集D的纯度越高。

选择使得划分后基尼指数最小的属性作为最优划分属性。

决策树生成

算法	特征选择
ID3	信息增益
C4.5	增益率
CART	基尼指数

决策树剪枝

pruning，防止过拟合。
两类，预剪枝 prepruning，后剪枝 postpruning。在 validation set 上验证泛化能力。

• 预剪枝，决策树生成过程中，对每个节点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前节点标记为叶节点。
• 后剪枝，先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能的提升，则将该子树替换为叶节点。

预剪枝

优点：预剪枝使得决策树的很多分支都没有展开，不仅降低了过拟合的风险，还显著减少了决策树的训练时间开销和调试时间开销。
缺点：Greedy。当前划分虽然泛化没增加，但可能是后续优秀划分的先决条件。可能欠拟合。

后剪枝

优点：会保留更多分支，欠拟合风险很小，泛化性能优于预剪枝决策树。
缺点：完全生成决策树后又自底向上对树中所有非叶子结点进行逐一考察，训练时间开销更大。

连续与缺失值

连续值处理：
连续属性离散化：如，二分法 bi-partition 对连续属性进行处理，相邻区间的中位点。C4.5
注意，与离散属性不同，若当前节点划分属性为连续属性，该属性还可作为其后代节点的划分属性。

缺失值处理：
定义训练集$D$和属性$a$，令$\tilde D$表示$D$中在属性$a$上没有缺失值的样本子集。

问题1：如何在属性值缺失的情况下进行划分属性选择？
只根据$\tilde D$来判断属性$a$的优劣。

问题2：给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？ C4.5
缺失值的存在被分为几个大小不同碎片，分别属于几个不同的阵营。
$w_x$是样本$x$的权重。
$\rho$表示无缺失值样本所占的比例，$\tilde \rho_k$表示无缺失值样本中的第k类所占的比例，$\tilde r_v$表示无缺失值样本中在属性a上取值$a^v$的样本所占的比例。


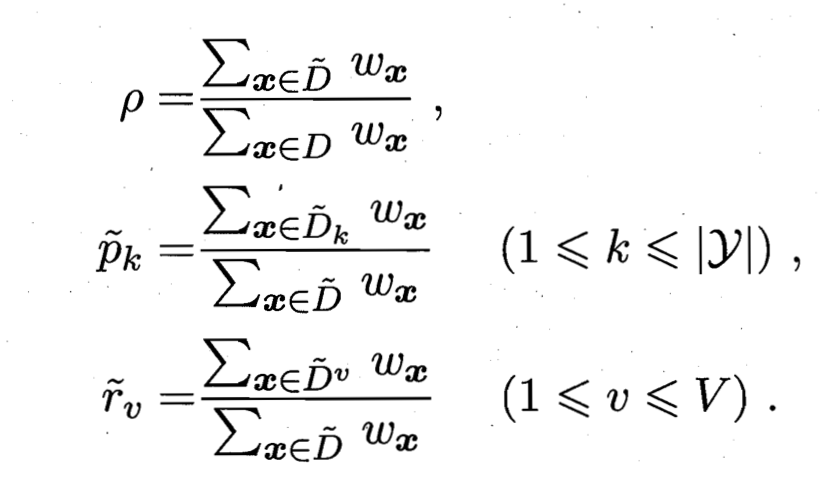
若样本$x$在划分属性$a$上的取值已知，则将$x$划入与其取值对应的节点，且样本权值在子节点中保持为$w_x$。若样本$x$在划分属性$a$上取值未知，则将$x$同时划入所有子节点，且样本权值在与属性值$a^v$对应的子节点中调整为$\tilde r_v \cdot w_x$。直观地看，这就是让同一个样本以不同的概率划入到不同的子节点中去。

多变量决策树

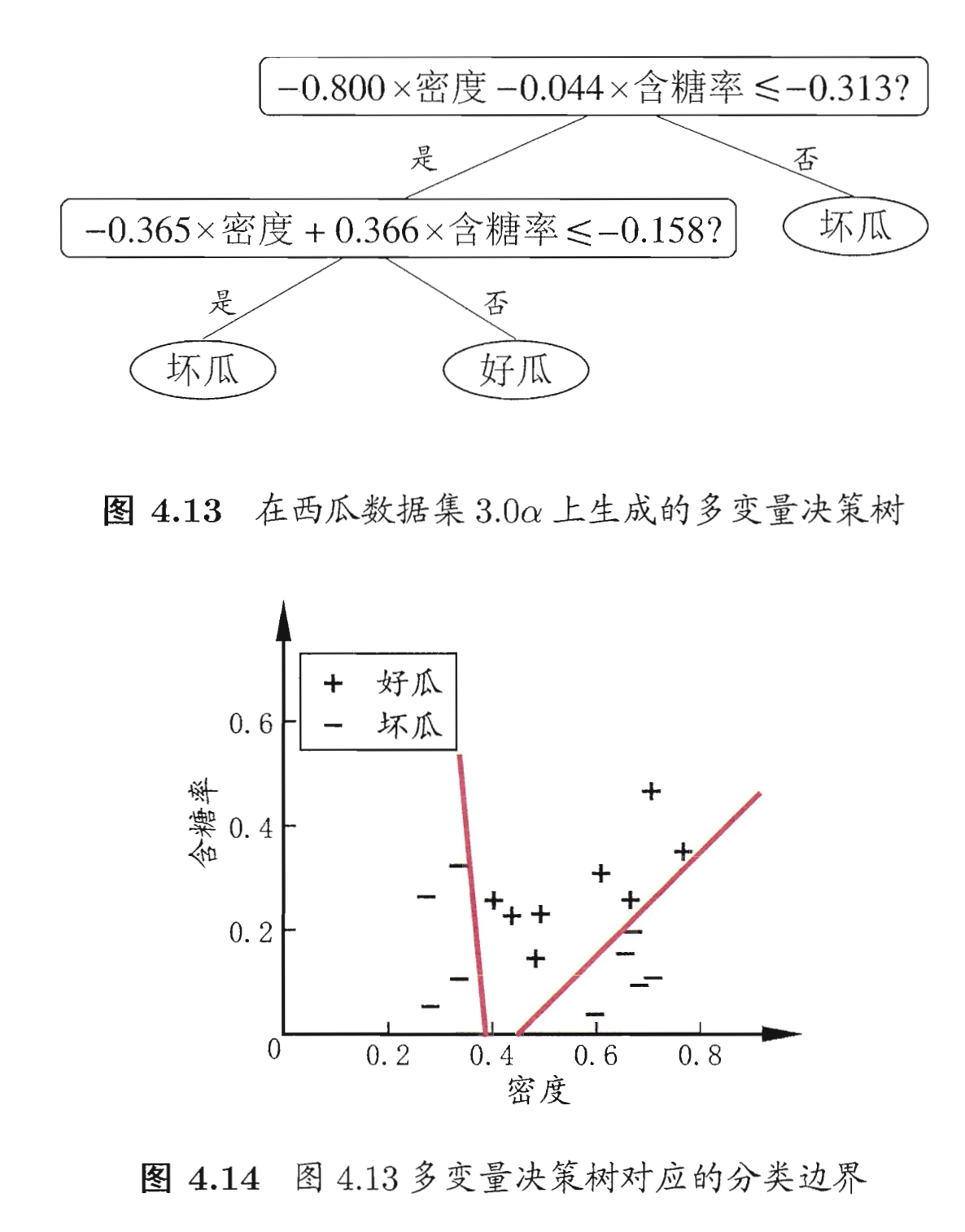
斜划分，不再是垂直划分。
非叶节点不再是仅对某个属性，而是对属性的线性组合进行测试。即，每个非叶节点是一个形如$\sum_{i=1}{d}w_i a_i = t$的线性分类器，其中$w_i$是属性$a_i$的权重，$w_i$和$t$可在该节点所含的样本集和属性集上学得。

Tree-Based Method 库

scikit-learn
dmlc XGBoost
Microsoft/LightGBM

Ref

[1] 机器学习 - 周志华
[2] 统计学习方法
[3] Coursera - How to Win a Data Science Competition
[4] Edx - Principles of Machine Learning