Logistic Regression 对数几率回归

Machine Learning

Logistic Regression

输出Y=1的对数几率lny1−yln \frac{y}{1-y}是由输入x的线性函数wTx+bw^Tx+b表示的模型。
Image Loading
适用问题：二类、多类分类任务
适用数据类型：数值型和标称型数据。
优点：计算代价不高，易于理解和实现；直接对分类可能性进行建模，无需实现假设数据分布，这样就避免了假设分布不准确所带来的问题；他不是仅预测出类别，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。
缺点：容易欠拟合，分类精度可能不高。
模型-知识表示：
模型-目标策略：极大似然估计
模型-损失函数：
模型-优化算法：梯度下降法、牛顿法

逻辑斯蒂分布

设XX是连续随机变量，如果随机变量XX对应的概率密度函数f(x)f(x)和累积分布函数F(x)F(x)分别是：

f(x)=e−x−μss(1+e−x−μs)2f(x) = \frac{e ^{- \frac{x - \mu}{s}}}{s(1 + e^{-\frac{x - \mu}{s}})^2}

F(x)=P(X≤x)=∫−∞xf(x)dx=11+e−x−μsF(x) = P(X \le x) = \int^{x}_{- \infty} f(x) dx = \frac{1}{1 + e^{-\frac{x - \mu}{s}}}

那么，XX服从逻辑斯蒂分布。其中，μ\mu为位置参数，s>0s \gt 0为形状参数。

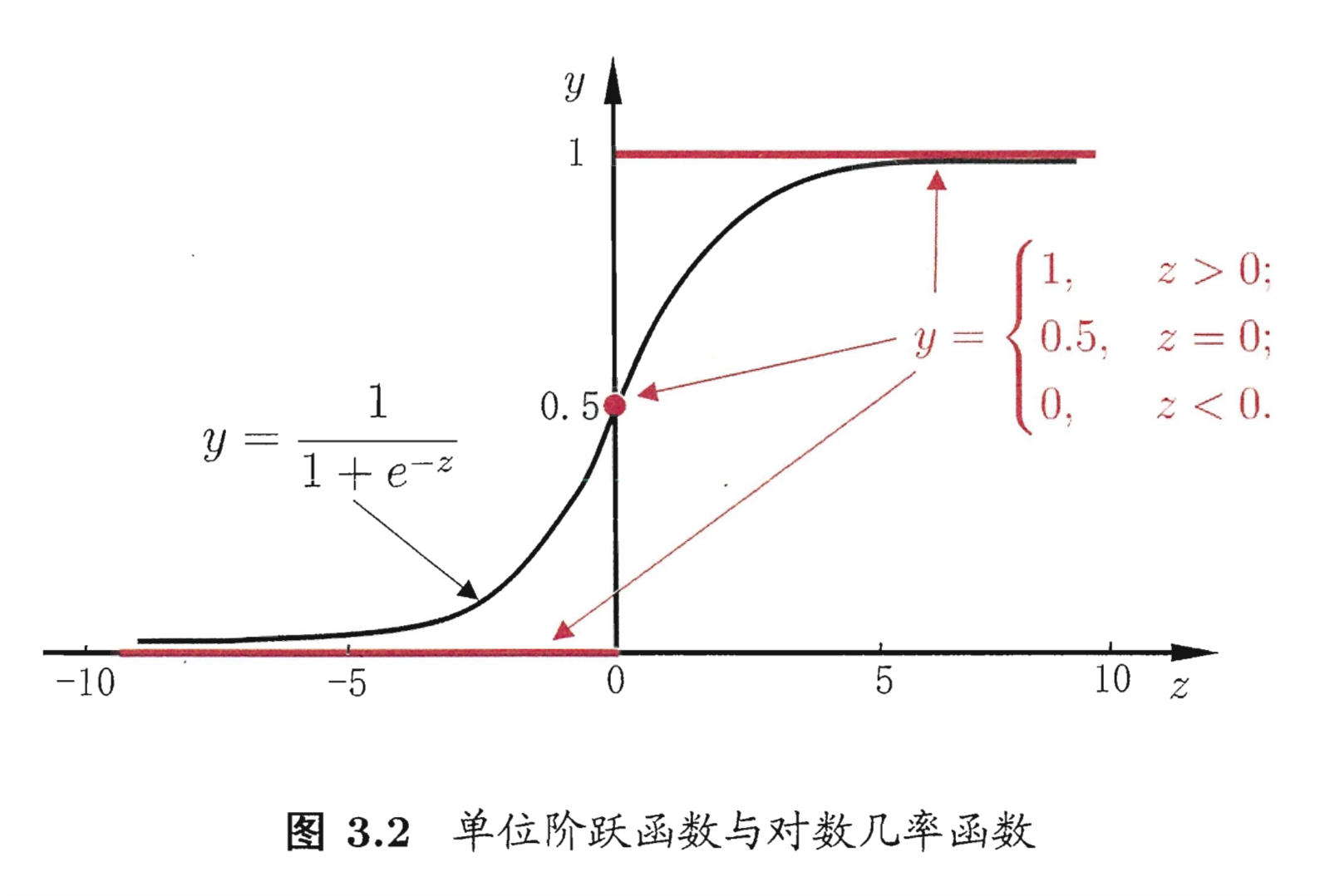
Image Loading
该累积分布函数是一条 Sigmoid 曲线。该曲线的特点是以点(μ,12)(\mu, \frac{1}{2})为中心对称。
曲线在中心附近增长较快，在两端增长速度较慢。从密度函数和分布函数图形都能看出，形状参数s的值越小，曲线在中心附近增长的越快。

逻辑斯蒂回归模型

前面介绍的线性回归，其应用场景大多是回归分析，一般不用在分类问题上。原因可以概括为以下两个：

  1. 回归模型是连续型模型，即预测出的值都是连续值（实数值），非离散值；
  2. 预测结果受样本噪声的影响比较大。

而本节要介绍的逻辑斯蒂回归模型（Logistic Regression Model，简称LR模型）是一种可用来分类的模型。在这里，自变量XX取值为连续值或离散值，因变量YY取值为1或0。

LR 模型表达式

LR模型表达式为参数化的逻辑斯蒂（累积）分布函数（默认参数μ=0,s=1\mu=0,s=1）即：

hw(x)=11+e−wT⋅xh_w(x) = \frac{1}{1 + e^{-w^T \cdot x}}

hw(x)h_w(x)作为事件结果y=1y=1的概率取值。这里，x∈Rn+1x \in R^{n+1} ,y∈(1,0)y \in {(1,0)}，w∈Rn+1w \in R^{n+1}是权值向量。其中权值向量ww中包含偏置项，即w=(w0,w1,…,wn)w=(w_0,w_1, \ldots ,w_n),$ x=(1,x_1, \ldots ,x_n)$。

理解 LR 模型

对数几率

一个事件发生的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是pp，那么该事件的几率为p1−p\frac{p}{1-p}，该事件的对数几率（log odds，用logit函数表示）是：

logit(p)=logp1−plogit(p) = \log \frac{p}{1-p}

对LR而言，由前两个公式得到：

loghw(x)1−hw(x)=wTx\log \frac{h_w(x)}{1- h_w(x)} = w^Tx

即在 LR 模型中，输出y=1y=1的对数几率是输入实例xx的线性函数。

将 logistic function 代入 GLM 的公式得到，
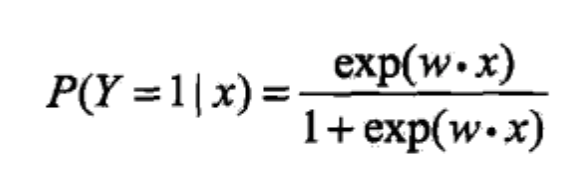
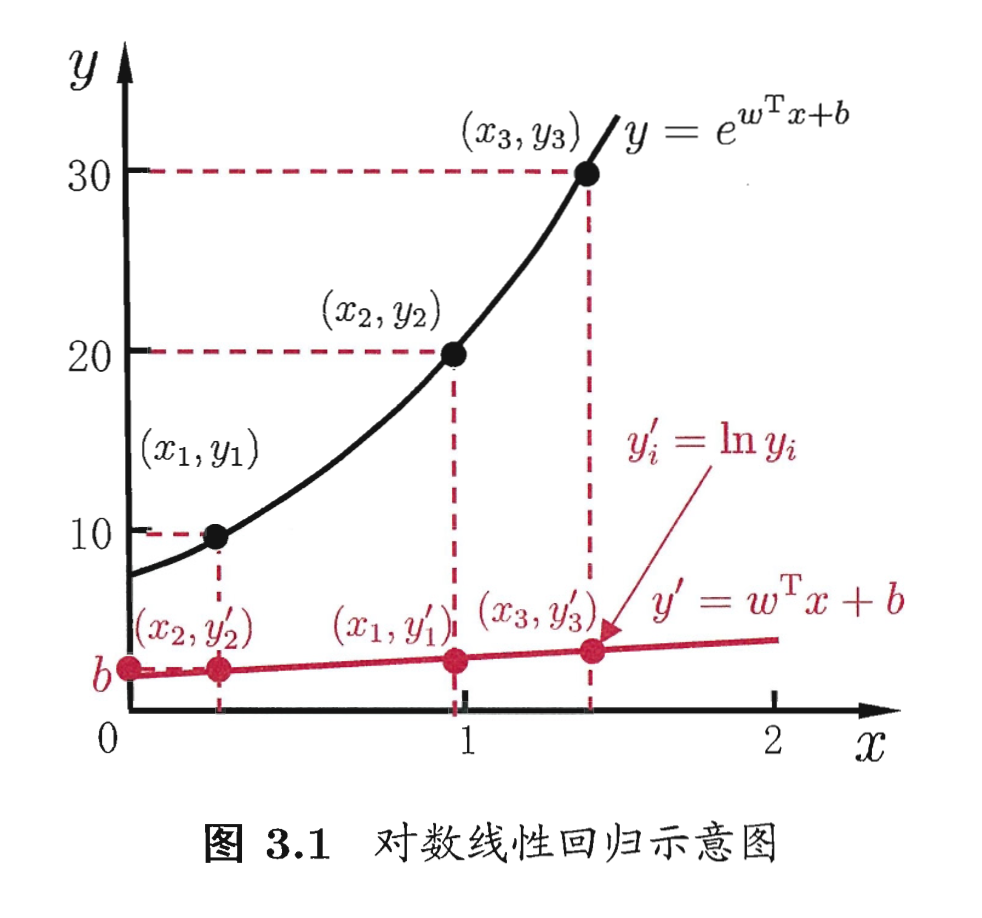
Image Loading
Image Loading
看3.18式，Logistic regression 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率。
看3.19式，yy即P(Y=1∣x)P(Y=1|x)，输出Y=1的对数几率lny1−yln \frac{y}{1-y}是由输入x的线性函数表示的模型。

函数映射

除了从对数几率的角度理解LR外，从函数映射也可以理解LR模型：

考虑对输入实例xx进行分类的线性表达式wTxw^Tx，其值域为实数域。通过 LR 模型表达式可以将线性函数wTxw^Tx的结果映射到(0,1)区间，取值表示为结果为1的概率（在二分类场景中）。
线性函数的值愈接近正无穷∞\infty，概率值就越接近1；反之，其值越接近负无穷，概率值就越接近0。这样的模型就是 LR 模型。

逻辑斯蒂回归本质上还是线性回归，只是特征到结果的映射过程中加了一层函数映射（即sigmoid函数），即先把特征/变量线性求和，然后使用sigmoid函数将线性和约束至(0,1)(0,1)之间，结果值用于二分或回归预测。

LR模型 - 概率解释

LR模型多用于解决二分类问题，如广告是否被点击（是/否）、商品是否被购买（是/否）等互联网领域中常见的应用场景。
但是实际场景中，我们又不把它处理成“绝对的”分类问题，而是用其预测值作为事件发生的概率。
这里从事件、变量以及结果的角度给予解释。

我们所能拿到的训练数据统称为观测样本。问题：样本是如何生成的？
一个样本可以理解为发生的一次事件，样本生成的过程即事件发生的过程。对于0/1分类问题来讲，产生的结果有两种可能，符合伯努利试验的概率假设。因此，我们可以说样本的生成过程即为伯努利试验过程，产生的结果（0/1）服从伯努利分布。这里我们假设结果为1的概率为hw(x)h_w(x)，结果为0的概率为1−h_w(x)。

那么，对于第ii个样本，概率公式表示如下：

P(y(i)=1∣x(i);w)=hw(x(i)P(y^{(i)} = 1 | x^{(i)};w) = h_w(x^{(i)}

P(y(i)=0∣x(i);w)=1−hw(x(i)P(y^{(i)} = 0 | x^{(i)};w) = 1 - h_w(x^{(i)}

合并起来得到第ii个样本正确预测的概率：

P(y(i)∣x(i);w)=(hw(x(i))y(i)⋅(1−hw(x(i))1−y(i)P(y^{(i)} | x^{(i)};w) = (h_w(x^{(i)})^{y^{(i)}} \cdot (1 - h_w(x^{(i)})^{1-y^{(i)}}

上式是对一条样本进行建模的数据表达。对于多条样本，假设每条样本生成过程独立，在整个样本空间中（m个样本）的概率分布为：

P(Y∣X;w)=∏i=1m((hw(x(i))y(i)⋅(1−hw(x(i))1−y(i))P(Y|X;w) = \prod^m_{i=1} ((h_w(x^{(i)})^{y^{(i)}} \cdot (1 - h_w(x^{(i)})^{1-y^{(i)}})

通过极大似然估计（Maximum Likelihood Evaluation，简称MLE）方法求概率参数。具体地，下面给出了通过随机梯度下降法（Stochastic Gradient Descent，简称SGD）求参数。

Image Loading

参数学习算法

Gradient Ascent

取对数方便计算，可得：

l(w)=logL(w)=∑i=1m(y(i)⋅log(hw(x(i)))+(1−y(i))⋅log(1−hw(x(i))))l(w) = \log L(w) = \sum_{i=1}^m (y^{(i)} \cdot \log(h_w(x^{(i)})) + (1 - y^{(i)}) \cdot \log(1 - h_w(x^{(i)})))

最大化log似然函数，就是最小化交叉熵误差（Cross Entropy Error）。

先不考虑累加和，针对每个参数wjw_j求偏导：
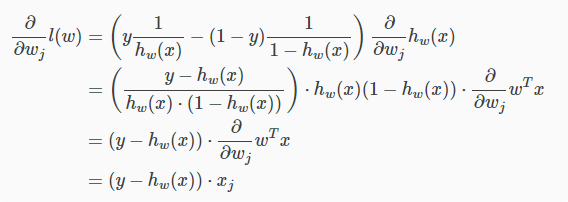
Image Loading

最后，通过扫描样本，迭代下述公式可求得参数：
用gradient ascent的方法，因为现在是要maximize a function了。
wj+1=wj+α⋅(y(i)−hw(x(i)))⋅xj(i)w_{j+1} = w_j + \alpha \cdot (y^{(i)} - h_w(x^{(i)})) \cdot x_j^{(i)}
α\alpha表示学习率。

用gradient ascent的方法，因为现在是要maximize a function了。

除此之外，还有Batch GD，共轭梯度，拟牛顿法（LBFGS），ADMM分布学习算法等都可用于求解参数。

Sigmoid 函数性质：

  1. hw(−x)=1−hw(x)h_w(-x) = 1 - h_w(x)
  2. hw′(x)=(1−hw(x))⋅hw(x)h'_w(x) = (1 - h_w(x)) \cdot h_w(x)

推倒：
Image Loading

Newton’s Method

Newton’s method, finding a zero of a function:
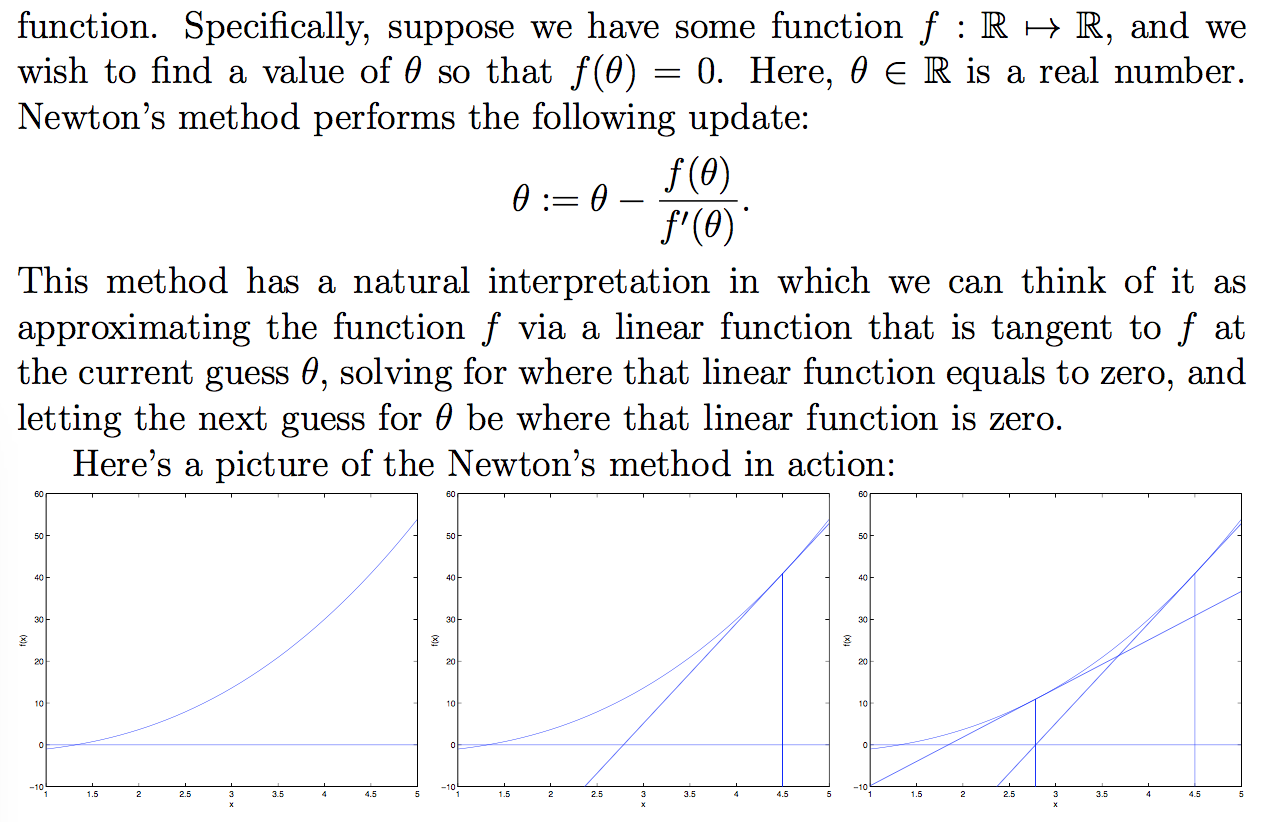
Image Loading
用Newton’s method来最大化方程l。l’为0时，l最大，令f(θ) = l′(θ)。
Image Loading
由于θ应该是向量：
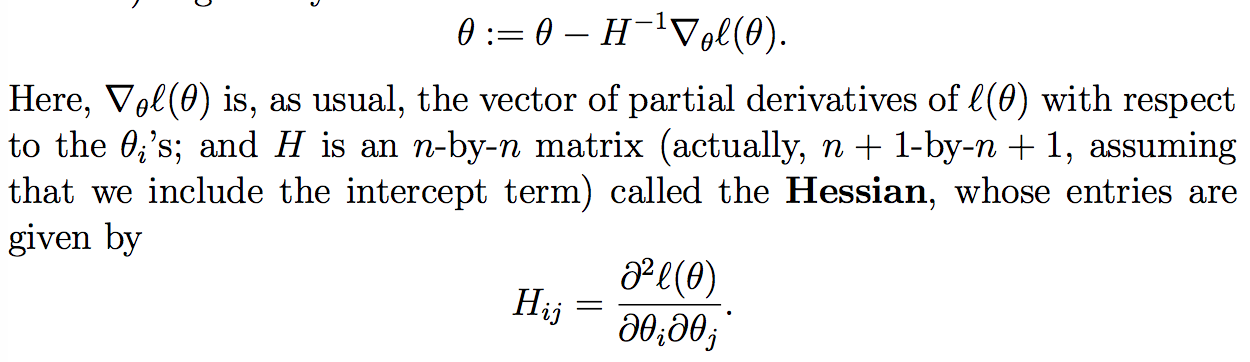
Image Loading
Newton’s method一般比batch gradient descent收敛快，不过每个iteration计算量大。
Newton’s method应用于最大化logistic regression log likelihood function l(θ)时，算法称为Fisher scoring。

多项 Logistic Regression

multi-nominal logistic regression model。
Image Loading
还是用极大似然估计。

LR 模型与广义线性模型、指数族分布

  • LR模型是广义线性模型的特例。
    当目标值分布服从伯努利分布时。
  • LR模型满足指数族分布。
    LR模型是指数族分布中y服从二项分布的特例。

LR 模型在工业界的应用

LR模型是工业界应用最多的模型之一，不管是在各种预估问题场景（如推荐、广告系统中的点击率预估，转化率预估等），亦或是分类场景（如用户画像中的标签预测，判断内容是否具有商业价值，判断点击作弊等等），我们发现都会出现LR的身影。

总结发现，LR模型自身的特点具备了应用广泛性。总结如下：

  • 模型易用：LR模型建模思路清晰，容易理解与掌握；
  • 概率结果：输出结果可以用概率解释（二项分布），天然的可用于结果预估问题上；
  • 强解释性：特征（向量）和标签之间通过线性累加与Sigmoid函数建立关联，参数的取值直接反应特征的强弱，具有强解释性；
  • 简单易用：有大量的机器学习开源工具包含LR模型，如sklearn、spark-mllib等，使用起来比较方便，能快速的搭建起一个learning task pipeline；

但在工业界中典型的大规模学习任务－如广告的CTR预估问题。除了预估模型自身外，还要考虑模型能否解决学习任务、业务场景中出现的问题。比如：

  • 学习的过拟合问题；
  • 学习的数据稀疏性问题；
  • 模型自身的学习效率（收敛速度，稳定性）；
  • 训练模型时数据、特征的扩展性问题，即学习算法可否在分布式环境下工作；
  • 如何结合实际应用场景（比如多资源位／多广告位的点击预估问题），给出相应的解决方案.

从模型的角度，过拟合和稀疏性问题可以在优化求解中的LR损失函数基础上加上正则项来解决：

  • loss function + λ∣w∣22\lambda |w|^2_2：解决过拟合。
  • loss function + λ∣w∣1\lambda |w|_1：解决稀疏性，比如Google13年出的预估方法－FTRL模型，虽然是在线学算法，但主要是为了解决预估时的稀疏性问题。

超大规模稀疏LR模型学习问题，LR模型自身是做不到的。这个时候需要我们为它选择一个学习算法和分布式系统。在分布式环境下，约束优化求解理想方案之一－ADMM算法（交叉方向乘子法），可用于求解形式为"loss function + 正则项"目标函数极值问题。

关于ADMM，这里给出简单的概括：

  1. ADMM算法在拉格朗日函数中引入惩罚函数项（二阶项）用于保证求解时的收敛效率（收敛速度）和结果的健壮性（放松目标函数为强凸的限制）。
  2. 目标函数可分的，可以将数据集划分多了数据block，各自学习得到局部参数，然后汇总得到全局参数；进一步将全局参数“广播”（broadcast）至各个计算节点，用于下一轮局部参数学习的初始值。
  3. ADMM算法框架将目标函数划分为两部分（为了引入全局参数），局部参数与全局参数的组合作为约束条件；算法自身结构也是为了适应在分布式环境下求解。

Ref

[1] 机器学习 - 周志华
[2] 统计学习方法
[3] http://www.52caml.com/head_first_ml/ml-chapter1-regression-family/#逻辑斯蒂回归（Logistic_Regression）
[4] cs229