Backtracing & Branch-and-Bound
回溯法和分支界限法
回溯法和分支界限法是两种算法设计技术,它们求解的是这种问题:随着实例规模的增长,问题的选择次数至少呈指数增长。两种算法每次都只构造解的一个分量,一旦确定当前已经做出的选择无法导出一个解,就会立即中止当前步骤。这种方法使我们能够在可接受的时间内,对NP困难问题的许多较大实例求解。
无论是回溯法还是分支界限法,都把状态空间树作为它们的主要机制。状态空间树是一棵有根树,它的节点代表了所讨论问题的部分构造解。一旦能够确认,从和节点子孙相对应的选择中无法求得问题的解,这两种技术都会立即中止该节点。
回溯法
回溯法在它的大多数应用中,都按照深度优先查找法构造它的状态空间树。如果状态空间树的当前节点所代表的选择序列可以进一步扩展,而且不会违反问题的约束,它就会考虑下一个分量的第一个余下的合法选择。否则,这个方法就会回溯,也就是撤销部分构造解的最后一个分量,并用下一个选择来代替。
回溯法构造了一棵状态空间树。树的根代表了在查找解之前的初始状态。树的第一层节点代表了对解的第一个分量所做的选择,第二层代表第二个,以此类推。树是按照深度优先的方法构造的。如果当前节点是有希望的,通过向部分解添加下一个分量的第一个合法选择,就生成了节点的一个子女,而处理也会转向这个子女节点。如果当前节点变得没希望了,该算法回溯到该节点的父母,考虑部分解的最后一个分量的下一个可能选择。如果这种选择不存在,它再回溯到树的上一层,以此类推。
- 回溯法主要用于那些困难的组合问题,这些问题可能存在精确解,但我们无法用高效的算法求解。
- 回溯法和穷举查找法是不同的。穷举查找法注定很缓慢,回溯法对于一些规模不是很小的实例,还是有一些希望可以在可接受的时间内求解的。
回溯法进行优化的几个技巧:利用组合问题中常常表现出来的对称性,比如4皇后不用考虑第一个放在后两列的情况。把值预先分配给解的一个或多个分量,比如子集和中用到预排序。
n皇后问题
n皇后问题是指把n个皇后放在的棋盘上,使得任意两个皇后不能同行、不能同列、也不能位于同一条对角线上。
考虑对4皇后问题求解:
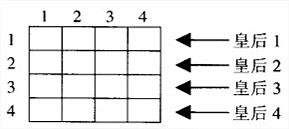
![]()
哈密顿回路问题
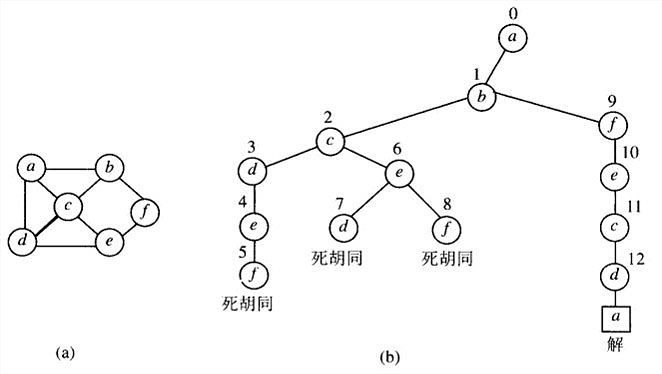
"子集和"问题
"子集和"问题:求n个正整数构成的一个给定集合S=\\{s_1,...,s_n\\}的子集,子集的和要等于一个给定的正整数d。例如,对于S={1,2,5,6,8}和d=9来说,该问题有两个解:{1,2,6}和{1,8}。
首先把集合元素按照升序排列。然后可以构造状态空间树了。在遍历的过程中,如果数字的和s’等于d,就是解。如果s’不等于d,下面这两个不等式中任何一个成立,这个节点就没有希望,终止掉。
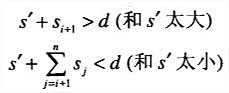
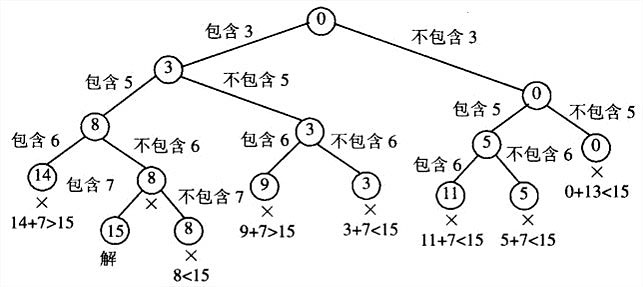
相关问题
- 插棒游戏。这个类似谜题的游戏在等边三角形的板上布置了15个孔。在初始的时候,如下图所示,除了一个孔,所有孔都插上了插棒。一个插棒可以跳过它的直接邻居,移到一个空白的位置上。这一跳会把被跳过的邻居从板上移走。
设计并实现一个回溯算法,求解该谜题的下列版本:
(a) 已知空孔的位置,求出消去13个插棒的最短步骤,对剩下的插棒的最终位置不限。
(b) 已知空孔的位置,求出消去13个插棒的最短步骤,剩下的插棒最终要落在最初的空孔上。

分支界限法
分支界限法是一种算法设计技术,它强化了状态空间树的生成方法。也就是估计可能从树的当前节点中求得的最佳值,如果这个估计值不超过当前过程中已经得到的最佳解,接下来就不会再考虑该节点了。
和回溯法相比,分支界限法需要两个额外的条件:
- 对于一棵状态空间树的每一个节点所代表的部分解,我们要提供一种方法,计算出通过这个部分解繁衍出的任何解在目标函数上的最佳值边界。
- 目前求得的最佳解的值。
分支界限法的主要思想是:拿某个节点的边界值和目前求得的最佳解进行比较,如果边界值不能超越目前的最佳解,这个节点就是一个没有希望的节点,需要立即中止,因为从这个节点生成的解,没有一个能比目前已经得到的解更好。
在下面3种情况下,终止在当前节点上的查找路径:
- 该节点的边界值不能超越目前最佳解的值。
- 该节点无法代表任何可行解,因为它已经违反了问题的约束。
- 该节点代表的可行解的子集只包含一个单独的点(因此无法给出更多的选择)。
分配问题
分配问题要求把n项工作分配给n个人,并使总分配成本尽可能地小。
分配问题可以转为这样描述:从成本矩阵C的每一行中选取一个元素,使得任何两个元素都不在同一列上,并使它们的和尽可能小。
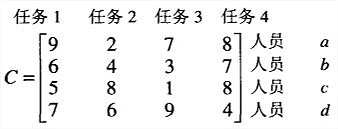
在构造状态空间树的时候,不同于回溯法总是生成最近一个有希望节点的单个子女,分支界限法在当前树的未终止叶子中,我们会选择其中最有希望的节点,并生成它的所有子女。
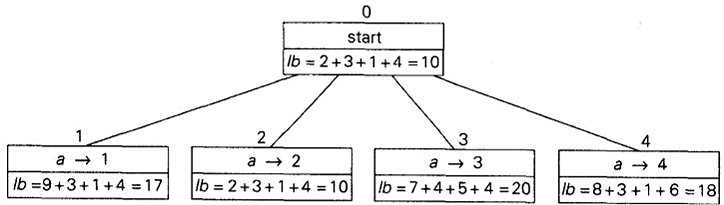
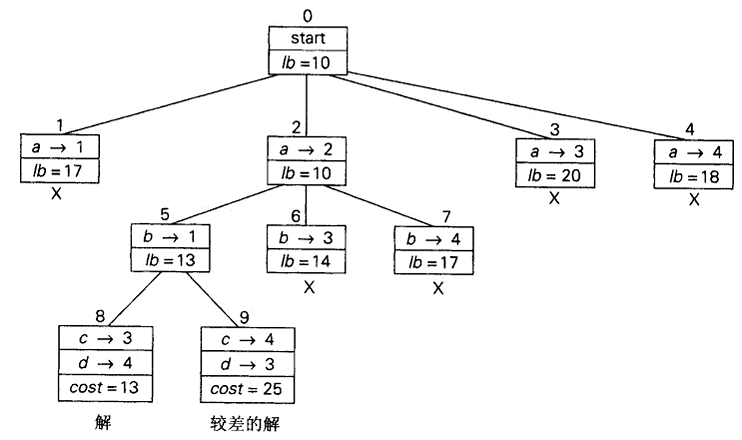
对于分配问题,有多项式时间解法的匈牙利法。所以分支界限法不作为实际应用。
背包问题
背包问题的介绍和动态规划的算法看这里。
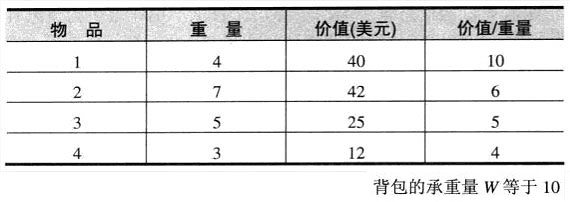
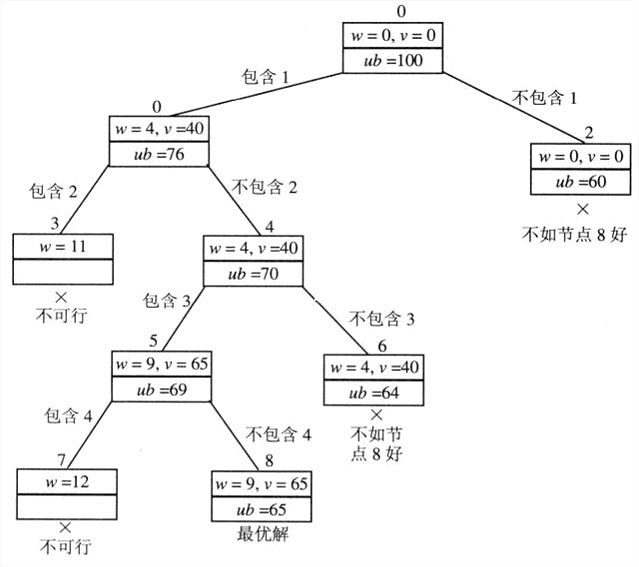
采用分支界限法时,先把实例中的物品按照v/w的值排序。这样,第一个物品可以给出每单位重量的最佳回报,而最后一个物品只能给出每单位重量的最差回报。
状态空间树中,向左的分支表示包含下一个物品,向右的分支表示不包含下一个物品。我们把这个选择的总重量w和总价值v,记录在节点中,有必要的话,任何向这个选择添加0个或者多个物品之后得到的子集的上界ub也记录下来。
计算上界ub的一个简单方法是,把已经选择物品的总价值v,加上背包的剩余承重量W-w与剩下物品的最佳单位回报的积:(公式总是渲染错误,i+1是下标)
旅行商问题
旅程长度l的下界有一种比较好的计算方法:对于每一个城市i,0<i<n+1,求出从城市i到最近的两个城市的距离之和;计算出这n个数字的和s,并把结果除以2。
如对图a中的实例,lb=[(1+3)+(3+6)+(1+2)+(3+4)+(2+3)]/2=14。
考虑以a为起点的旅程。因为图是无向图,可以只生成b在c之前的旅程。在访问n-1=4个城市之后,我们的旅程只能访问那个没有被访问的城市,然后回到起点,没有别的选择。
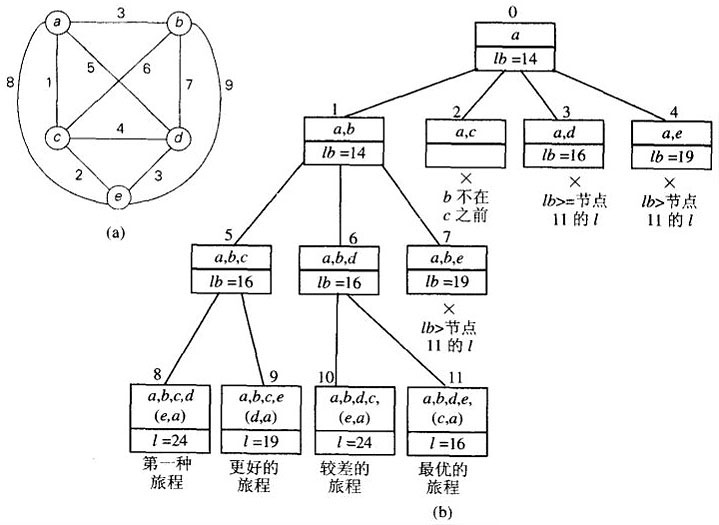
每个状态在确定一条路线后,计算lb时选择的两条路线是确定的那条和剩下最小的那条。
人工智能的一个分支特别关心生成状态空间树的不同策略。
NP困难问题的近似算法
启发式算法是一种来自于经验而不是来自于数学证明的常识性规则。
近似算法常常用来求组合优化难题的近似解。性能比是用来衡量这种近似算法精度的主要量度。
相关问题
广度优先搜索
Word Ladder
Word Ladder II
Surrounded Regions
深度优先搜索
一般套路是:检查是否满足收敛条件,是否满足终止条件,剪枝,进行下一步深搜。
常常与备忘录法结合,记录一些中间计算结果。
Palindrome Partitioning
Unique Paths
Unique Paths II
N-Queens
N-Queens II
Restore IP Address
Combination Sum
Combination Sum II
Generate Parentheses
Sudoku Solver
Word Search
[Brute Force] | Combinations
[Brute Force] | Letter Combinations of a Phone Number
[Tree] | Path Sum II
[1] 算法设计与分析基础(第2版)
[2] leetcode