Iterative Improvement

迭代改进

迭代改进技术用来求最优问题的解，它生成一系列使问题的目标函数值不断改进的可行解。这一系列的可行解中，后续解相比前面的解一般总是有些小的、局部的改变。如果目标函数值无法再得到优化，该算法就把最后的可行解作为最优解返回，然后算法就结束了。
正好可以用迭代改进算法求解的重要问题包括线性规划、网络流量最大化以及图的最大数量顶点匹配问题。

单纯形法

单纯形法是求解一般线性规划问题的经典方法。它的思路是：生成问题可行区域的一系列邻接极点，使得目标函数值不断改进。

线性规划问题定义

之前已经介绍过线性规划问题的定义，见变治法中问题化简思想下线性规划一节。
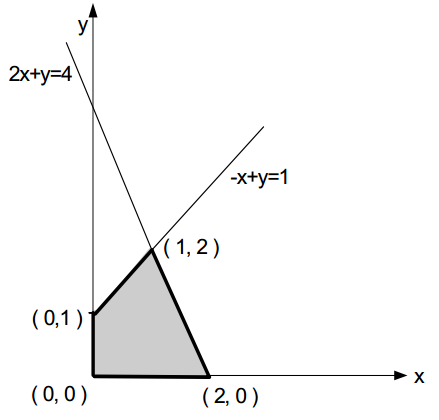
线性规划问题的例子：考虑下列两个变量的线性规划问题。求3x+5y的最大或最小值。

用图示的方法解决：

可行区域的顶点称为极点。可以得到定理：可行区域非空的任意线性规划问题有最优解，而且，最优解总是能够在其可行区域的一个极点上找到。
坏消息是：随着问题规模的增长，极点的数量是指数级增长的。此时对极点穷举就不现实了。

单纯形法解线性规划问题

好消息是：单纯形法可以在一般情况下只需要检测可行区域极点中的一小部分就能找到最优点。
算法的思想可以用几何术语描述：现在可行区域中找到一个极点。然后检查一下是不是在邻接极点处可以让目标函数取值更佳。如果不是，当前顶点就是最优点，然后算法停止；如果是，转而处理那个能让目标函数取值更佳的邻接顶点。有限步以后，该算法要么发现了一个取到最优解的极点，要么证明了最优解不存在。

步骤：

1. 初始化。将给定的线性规划问题表示成标准形式，并建立一个初始表格，它最右列的单元格都是非负的，接下来的m列组成了一个$m\times m$的单位矩阵(目标行的单元格则不必满足这一条件)。这m列确定了初始的基本可行解的基本变量，而表格中的行用基本变量来标识。
2. 最优测试。如果目标行中的所有单元格都是非负的(除了最右列中代表目标函数值的那个单元格)，就可以停止了：该表格代表了一个最优解，它的基本变量的值在最右列中，而剩下的非基本变量的值是0。
3. 确定输入变量。从目标行的前n个单元格中选择一个非负的单元格(一个常用规则是，选择绝对值最大的那个负单元格，至于是哪个单元格则无关紧要)。该单元格所在的列确定了输入变量和主元列。
4. 确定分离变量。对于主元列上的每个正单元格，将其所在行最右单元格除以主元列的单元格，求得一个所谓的$\Theta$比率(如果主元列单元格都为负或0，该问题是无界的，算法终止)。找出$\Theta$比率最小的行，该行确定了分离变量和主元行。
5. 建立下一张表格。将主元行中的所有单元格除以主元得到新主元行。包括主元行在内的每一行，要减去该行主元列单元格和新主元行的乘积(除了主元行的1，这一步会把主元列的所有单元格变成0)。把主元行前的标识用主元列的变量名代替，返回第0步。

一个例子


用单纯形法。

然后计算表格。每个约束一行，目标将参数取反一行，并代入初始基本可行解(0,0,1,4)。
取目标行负值最大的一列为主元列。
对于主元列上的每个正单元格，将其所在行最后一个单元格除以主元列的单元格，求得$\theta$比率。比率最小的行是主元行。
将主元行中所有单元格除以主元(主元是主元行和主元列的相交单元格)。
其他行的每个单元格减去自己主元列单元格与新的主元行本列的乘积。如uy上，1-(-1)*(1/2)= 3/2。
当目标行没有负数时，目标行最后一列的数就是最优解。

最优解是x=2,y=0，最大值为6。

相关问题

1. 议会绥靖。在一个议会中，每个议员最多有三个政敌。设计一个算法把议会分成两个议院，使得一个议员在所在议院中没有一个以上的政敌。
   思路：先将议员随机分为两院。遍历一遍，如果某个议员在自己院有两个政敌的话，就把他分到另一个院。于是自己和自己的政敌都得到解脱，每次减少至少一个政敌组。设一共有p对同议院政敌组，小于p次遍历即可完成。

最大流量问题

最大流量问题要求找出一个网络中可能存在的最大流量，网络是包含一个源点和一个汇点的加权有向图。

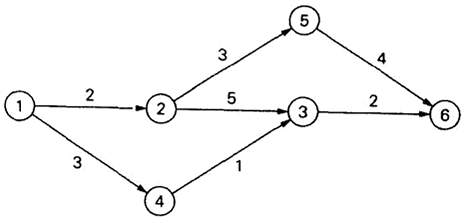
源点和汇点分别是物质流唯一的出发地和目的地，所有其他的顶点只能改变流的方向，但不能消耗或者添加物质。流量守恒要求。
根据流量守恒要求，最大流量问题可以这样定义：

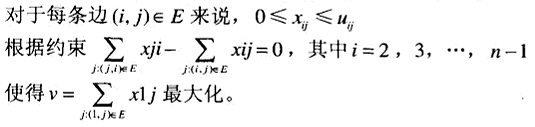
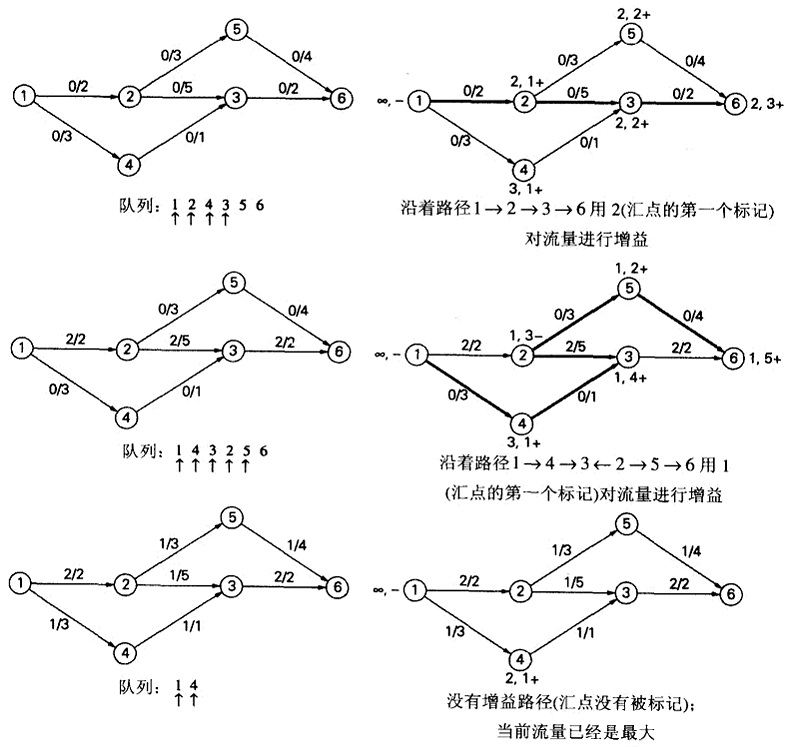
Ford-Fulkerson法是利用迭代改进技术求解最大流量问题的经典方法。最短增益路径法通过一种广度优先查找的方式对网络的顶点做标记，从而实现了上述思想。

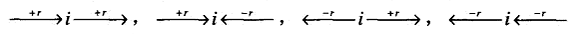
首先将网络中的每条边都设为0，然后在每次迭代时试着找到一条可以传输更多流量的从源点到汇点的路径，即增益路径。

最短增益路径法利用广度优先查找，用数量最少的边来生成增益路径。
用两个记号来标记一个新的(未标记)顶点。第一个标记指出从源点到被标记顶点还能增加多少流量。第二个标记指出另一个顶点的名字，就是从该顶点访问到被标记顶点的。前向边为+，后向边为-。

• 首先将源点入队列，对其所有有残留流量的邻接点进行标记，先标记所有经前向边到达的，再标记所有经后向边到达的，首点出队列。把这些新标记的点加入队列。继续取出首点，遍历，直到队列为空。
• 然后根据汇点的第二个标记，反向推出路径，用第一个标记更新路径上的容量。
• 除了源点，所有标记擦除，重复上面过程。如果一次迭代后汇点没有被标记，那就是最优了。
  

1

// TODO

相关问题

1. 考虑网络是有根树的情况，它的根是源点，叶子是它的汇点，所有的边都是和从根到叶子的路径同向的。设计一个高效的算法来求出这种网络的最大流量。时间效率是什么。
   思路：见伪代码。
   

2. 就餐问题。几个家庭一起外出就餐。为了增进社交，他们希望同一个家庭的人不要坐在一张桌子上。试述如何利用最大流量问题找到一个满足要求的座位排法(或者证明这种排法不存在)。假设该就餐团具有p个家庭、第i个家庭有$a_i$个成员。还假设有q张桌子，第j张桌子的座位容量是$b_j$。
   思路：用如下图进行计算。
   
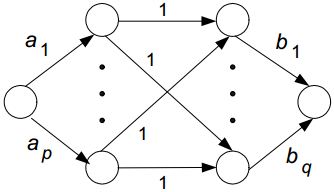
   如果求得的最大容量等于$a_1$到$a_p$所有家庭的人数之和，就是有解。

二分图的最大匹配

最大基数匹配是图中边的最大子集，该子集中的任何两条边都不共顶点。对于二分图来说，可以对之前求得的匹配进行一系列增益来获得这个子集。

在一个二分图中，所有的顶点都可以分为两个不相交的集合V和U，两个集合大小不一定相等，但每条边都连接两个集合中各一个顶点。

匹配的方式就是从两边子集各拿一个可以连接的自由顶点连接。
算法思路：大概就是某集合U自由的遍历所有可能的匹配，发现对方V也自由就赶紧连接；发现对方V不自由就宣布要争抢，让其考虑。对方V答应考虑，并叫自己的原始匹配U决定行不行。被叫到的U如果有替补的自由V匹配就结成新对，让原来配对的V和争抢的U结对；如果没有替补的自由V就不肯变化。遍历U中所有的自由节点，直到没有为止。
具体到本例：

• 选择V的所有自由顶点放进队列。队首弹出1，查找在U中与1相连的所有顶点遍历，先走到6，发现其自由。加(1,6)到M。删去所有标记。将队列重新初始化为V中的所有自由顶点，即2,3。退出遍历。
• 队首弹出2，查找U中与2相连的所有顶点遍历，遍历到6发现其不自由，标记6说2要6，并把6放入队列让其以后看着办。走到3，3遍历到6，发现6已被标记，再遍历到8，标记8为3。走到6，6说我是U集的，我想让原来和我匹配的1再考虑考虑，给1标记上6，把1放入队列。走到8，8也是U集，让4考虑，放入队列。走到1，1遍历到6，无事，遍历到7，发现7自由，加入(1,7)到M，这时1发现自己被6标记了，就从M中去掉(1,6)组合，让6被标记的(2,6)组合加入M。删去所有标记。将队列重新初始化为V中的所有自由顶点，即3。退出遍历。
• 队首弹出3，查找U中与3相连的所有顶点遍历，遍历到6发现其不自由，标记6说3要6，并把6放入队列让其考虑，继续遍历到8，发现8也不自由，标记8说3要8，把8放进队列让其考虑。走到6，6是U集的，标记原来匹配的2一个6，把2放入队列考虑。走到8，8是U集的，标记原来匹配的4一个8，放入队列重新考虑。走到2，2走到6无事，又没有下一个选择让其发现不对，就没变化。走到4，4经过8无事，遍历到9发现其不自由，标记9说4要9，把其放入队列考虑，遍历到10发现其自由，立刻结组(4,10)放入M，此时发现自己被8标记了，就放(3,8)进M。删去所有标记。将队列重新初始化为V中的所有自由顶点，为空。退出遍历。
  

1
2

相关题目

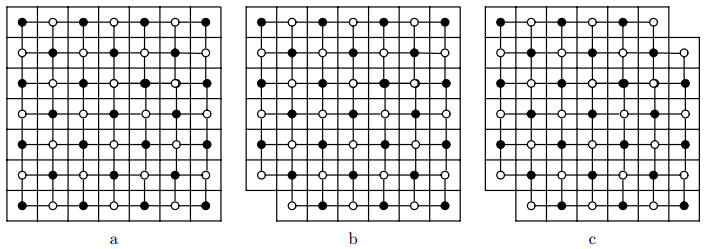
1. 多米诺谜题。多米诺是一块$2\times1$的方块，方向上既可以水平放置也可以垂直放置。一块由多个$1\times1$的格子组成的板，如果能够正好用多米诺覆盖，而且没有重叠，则称为一个覆盖。对于下面的板，确定它是不是可以用多米诺覆盖。如果是，之处如何覆盖；如果否，说明为什么。
   
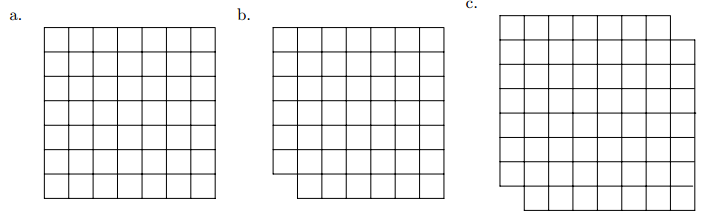
   解答：
   a. 不能。$7\times7$的总数是奇数，不是2的倍数。
   b. 能。对于2n某列缺1的板子总是可以。如图。
   
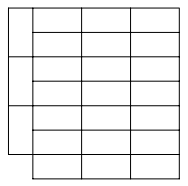
   c. 不能。把格子交错变成一黑一白相连，一个多米诺每次覆盖一个黑点一个白点。本例中是32个白点，30个黑点，无法覆盖。其他两问也可用这个方法解决。
   

稳定婚姻问题

稳定婚姻问题要求基于给定的匹配优先级，求出两个n元素集合的元素之间的稳定匹配。该问题可以用稳定婚姻算法求解，而且总有解。是二分图匹配问题的一个有趣版本。

有一个n个男士的集合Y=\\{m_1,m_2,..,m_n\\}和一个n个女士的集合X=\\{w_1,w_2,..,w_n\\}。每个男士有一个排序的列表，把女士按照潜在结婚对象的优先级进行排序。同样，每个女士也有一个男士的优先级列表。一对一进行匹配。如果在匹配M中，某男士和某女士都更倾向于对方而不是自己的匹配对象，称为受阻对。那么M就是不稳定的。稳定婚姻问题就是要根据给定的男士和女士的优先选择，求出一个稳定的婚姻匹配。

稳定婚姻算法
输入：有一个n个男士的集合和一个n个女士的集合，以及每个男士选择女士的优先级和每个女士选择男士的优先级。
输出：一个稳定的婚姻匹配。
第0步：一开始所有的男士和女士都是自由的。
第1步：如果有自由男士，从中任选一个然后执行以下步骤：

• 求婚：选中的自由男士m向w求婚，w是他优先列表上的下一个女士(即优先级最高而且之前没有拒绝过他)。
• 回应：如果w是自由的，她接受求婚和m配对。如果她不是自由的，她把m和她当前的配偶作比较。如果她更喜欢m，她接受m的求婚，她的前配偶就变成自由人。否则，她拒绝m的求婚，m还是自由的。

第2步：返回n个匹配对的集合。

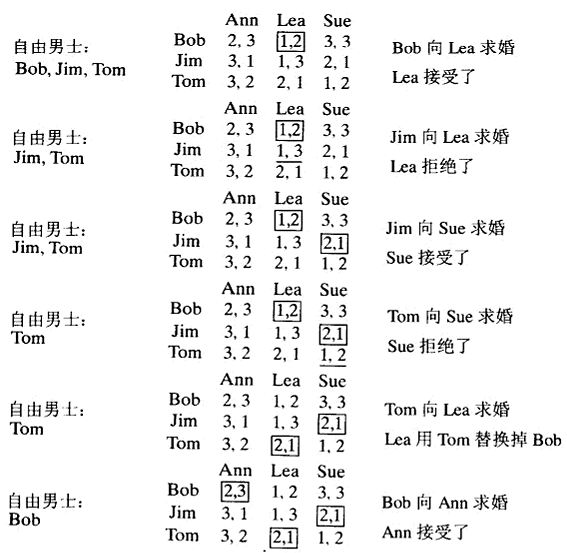
稳定婚姻算法有一个明显的缺陷，有“性别倾向”。它更容易满足男士的偏好。

[1] 算法设计与分析基础(第2版)