Space and Time Trade-Offs

Algorithm, C++

时空权衡

算法设计中的时空权衡是一个众所周知的问题。在应用中，空间换时间比时间换空间普遍得多。

空间换时间技术有两种主要的类型：

  1. 输入增强。思想是对问题输入的部分或全部做预处理，然后对获得的额外信息进行存储，以加速后面问题的解决。用分布计数进行排序以及一些重要的字符串匹配算法都是基于这个技术的算法。
  2. 预构造。使用额外的空间来实现更快和更方便的数据存取。散列和B树是预构造的重要例子。
  3. 还有一种相关的技术动态规划，是把给定问题中重复子问题的解记录在表中，然后求得所讨论问题的解。关于动态规划的详细讲解看这里。

注意，时间和空间并不是此消彼长的关系，如果选用了一种空间效率很高的数据结构来表示问题的输入，这种结构反过来又能提高算法的时间效率。比如稀疏图和稠密图应该分别用邻接链表和邻接矩阵。

计数排序

分布排序是一种特殊的方法，用来对元素取值来自于一个小集合的列表排序。

例如：对于下面的数组。
示例数组
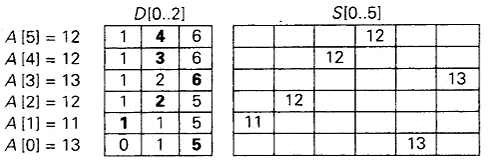
我们知道它们的值来自于集合{11,12,13}，并且在排序的过程中不能改写。下面是它们的频率数组和分布数组：
频率数组和分布数组
分布值指出了在最后的有序数组中，它们的元素最后一次出现时的正确位置。
处理过程：从右到左处理数组。最后的值是12，因为它的分布值是4，把这个12放到数组S的第3个位置上(S将会存放有序列表)。把12的分布值减1，再处理给定数组中的下一个(从右边数)元素。
用分布计数法排序的例子。减一的分布值用粗体字表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <vector>
#include <iostream>
#include <iterator>
#include <algorithm>
using namespace std;
//---------------------------------------------------
void distribution_counting(const vector<int>& origional, int min_num, int max_num, vector<int>& result)
{
	// 用分布计数法，对来自于有限范围整数的一个数组进行排序
	// 输入：数组origional，数组中的整数位于min_num和max_num之间
	// 输出：origional中元素构成的非降序数组result
	result.resize(origional.size());
	vector<int> distribution(origional.size());	// 初始化频率数组
	for (int i = 0; i < origional.size(); ++i)	// 计算频率值
	{
		++distribution[origional[i]-min_num];
	}
	for (int i = 1; i <= max_num - min_num; ++i)	// 重用于分布
	{
		distribution[i] += distribution[i-1];
	}
	for (int i = origional.size()-1; i >= 0; --i)
	{
		int index(origional[i]-min_num);
		result[distribution[index]-1] = origional[i];
		--distribution[index];
	}
	copy(result.begin(), result.end(), ostream_iterator<int>(cout, " "));
	cout << endl;
	system("Pause");
}
//---------------------------------------------------
int main()
{
	vector<int> origional(6, 12);
	origional[0]=13;
	origional[1]=11;
	origional[3]=13;
	vector<int> result;
	distribution_counting(origional, 11, 13, result);
}

这是一个线性效率的算法，仅对输入数组从头到尾连续处理两边。它的高效是因为空间换时间，以及输入列表独特的自然属性。

相关题目

  1. 设计一个只有一行语句的算法，对任意规模为n、元素值是n个从1+x到n+x的不同整数的数组排序。
1
for (int i = 0; i < n; ++i) {S[A[i]-1] = A[i];}
  1. 下面这个技术称为虚拟初始化。如果仅仅对一个给定数组A[0…n-1]中的某些元素进行初始化，这是一种时间效率很高的方法。对于数组的每一个元素，这个方法可以在常数时间内告诉我们，该元素是不是被初始化了；如果是，它的值是什么。这是因为该方法使用了一个变量counter来表示A中已初始化元素的个数，外加两个大小相同的辅助数组，比如说是B[0…n-1]和C[0…n-1]。这两个数组是这样定义的。B[0]，…，B[counter-1]包含了A中已初始化元素的下标：B[0]包含了第一个已初始化元素的下标，B[1]包含了第二个已初始化元素的下标，以此类推。而且，如果A[i]是第k个已初始化的元素(0<=k<=counter-1)，C[i]包含k。
    下面3个赋值操作完成后，描述数组ABC的状态。以及我们如何确定A[i]已经被初始化了。
    A[3]=x;A[7]=z;A[1]=y;
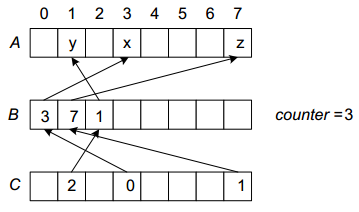
    数组ABC的状态
    确定A[i]已被初始化的方式：0⩽C[i]⩽counter−10 \leqslant C[i] \leqslant counter-1 && B[C[i]]==iB[C[i]]==i

字符串匹配中的输入增强技术

在一个较长的n个字符的串(文本)中，寻找一个给定的m个字符的串(模式)。它的蛮力解法在这里。
用于字符串匹配的Horspool算法可以看作是Boyer-Moore算法的一个简化版本。两个算法都以输入增强思想为基础，并且从右到左比较模式中的字符。两个算法都是用同样的坏符号移动表。Boyer-Moore算法还使用了第二个表，称为好后缀移动表。

Horspool算法

例子：考虑在某个文本中查找模式BARBER:
在某个文本中查找模式BARBER
从模式的最后一个R开始从右向左，比较模式和文本中的相应字符对。如果模式中所有的字符都匹配成功，就找到了一个匹配的子串。然而，如果遇到了一对不匹配字符，就需要把模式右移，希望移动幅度尽可能大。假设文本中，对齐模式最后一个字符的元素是字符c，Horspool算法根据c的不同情况来确定移动的距离。
一般来说，存在下面4种情况。

  • 情况1：如果模式中不存在c(本例中，c就是字母S)，模式安全移动的幅度就是它的全部长度(如果我们移动的幅度较小，模式中的某些元素还是会和字符c对齐，而c又不在模式中)。
    情况1
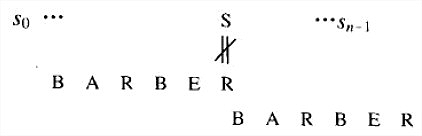
  • 情况2：如果模式中存在c，但它不是模式的最后一个字符(本例中，c就是字母B)，移动时应该把模式中最右边的c和文本中的c对齐：
    情况2
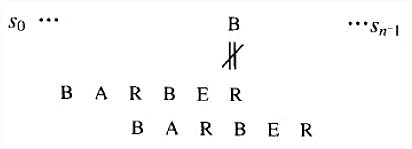
  • 情况3：如果c正好是模式中的最后一个字符，但是在模式的其他m-1个字符中不包含c，移动的情况就类似于情况1：移动的幅度等于模式的全部长度m。例如：
    情况3
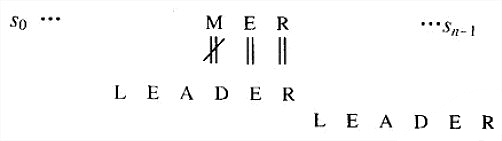
  • 情况4：如果c正好是模式中的最后一个字符，而且在模式的前m-1个字符中也包含c，移动的情况就类似于情况2：移动时应该把模式中前m-1个字符中的c和文本中的c对齐。
    情况4

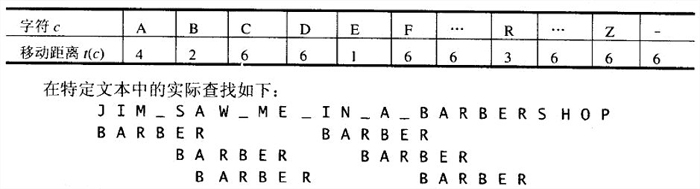
这个算法明显比蛮力算法对模式移动得更远。但是，如果这个算法在每次尝试的时候都必须检查模式中的每个字符，也会很慢，我们可以预先算出每次移动的距离并把它们存在表中。这个表是以文本中所有可能遇到的字符为索引的，内容是每个字符对应的模式移动的距离。
模式移动距离可以这样计算：
计算模式移动距离

Horspool算法总结

  1. 对于给定的长度为m的模式和在模式及文本中用到的字母表，按照上面的描述构造移动表。
  2. 将模式与文本的开始处对齐。
  3. 重复下面的过程，直到发现了一个匹配子串或者模式到达了文本的最后一个字符以外。从模式的最后一个字符开始，比较模式和文本中的相应字符，直到：要么所有m个字符都匹配(然后停止)，要么遇到了一对不匹配的字符。在后一种情况下，如果c是当前文本中和模式的最后一个字符相对齐的字符，从移动表的第c列中取出单元格t©的值，然后将模式沿着文本向右移动t©个字符的距离。

一个例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <vector>
#include <string>
#include <unordered_map>
#include <iostream>
using namespace std;
//---------------------------------------------------
void shift_table(const string& pattern, unordered_map<char, int>& table)
{
	// 用horspool算法和boyer-moore算法填充移动表
	// 输入：模式以及一个可能出现字符的字母表
	// 输出：以字母表中字符为索引的数组table
	for (int i = 0; i < pattern.size()-1; ++i)
	{
		//table.insert(make_pair(pattern.at(i), pattern.size()-1-i));
		table[pattern.at(i)] = pattern.size()-1-i;
	}
}
//---------------------------------------------------
int horspool_matching(const string& pattern, const string& text)
{
	// 实现horspool字符串匹配算法
	// 输入：模式pattern和文本text
	// 输出：第一个匹配子串最左端字符的下标，如果没有匹配子串，返回-1
	if (pattern.empty()) return 0;
	if (text.empty()) return -1;
	unordered_map<char, int> table;
	shift_table(pattern, table);	// 生成移动表
	int i = pattern.size()-1;	// 主字符串上模式最右端所对齐的位置
	while (i < text.size())
	{
		int matched_index(0);	// 匹配字符的个数
		while (matched_index < pattern.size() && pattern.at(pattern.size() - 1 -matched_index) == text.at(i - matched_index))
		{
			++matched_index;
		}
		if (matched_index == pattern.size())
		{
			return i - matched_index + 1;
		}else
		{
			i += table.count(text[i]) ? table[text[i]] : pattern.size();
		}
	}
	return -1;
}
//---------------------------------------------------
int main()
{
	string pattern("BARBER");
	string text("JIM_SAW_ME_IN_A_BARBERSHOP");
	cout << "find " << pattern << " in " << text << " : " << horspool_matching(pattern, text) << endl;
	system("Pause");
}

Boyer-Moore算法

与Horspool的相同之处：如果模式最右边的字符和文本中相应字符c所做的初次比较失败了，处理操作一致；也预先计算移动表。
与Horspool的不同之处：在遇到一个不匹配字符之前，如果已经有k(0<k<m)个字符成功匹配了，Boyer-Moore会参考两个数值来确定移动的距离。

  • 第一个数值是由文本中的一个字符c所确定的，它导致了模式中的相应字符和它不匹配。称为坏符号移动。导致这种移动的原因和导致Horspool算法移动的原因是一样的。计算方法是：如果这个数值是正数，它等于shift_table©-k；如果是0或者负数，则为1。即d_1=max\\{t_1(c)-k,1\\}。
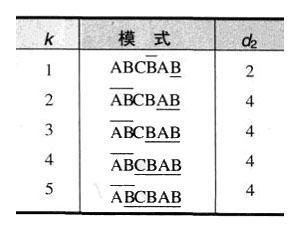
  • 第二个数值是由模式中最后k>0个成功匹配的字符所确定的。我们把模式的结尾部分叫作模式的长度为k的后缀，记作suff(k)。称为好后缀移动。移动的距离是从右数第二个suff(k)(它的后继字符和最后一个suff(k)的后继不同)到最右边的suff(k)之间的距离。即好后缀之间相隔的距离。如果不存在另一个suff(k)，就减少k值继续寻找。
    ABCBAB模式的好后缀表

Boyer-Moore算法总结

  1. 对于给定的模式和在模式及文本中用到的字母表，按照给出的描述构造坏符号移动表。
  2. 按照给出的描述，利用模式来构造好后缀移动表。
  3. 将模式与文本的开始处对齐。
  4. 重复下面的过程，直到发现了一个匹配子串或者模式到达了文本的最后一个字符以外：从模式的最后一个字符开始，比较模式和文本中的相应字符，直到要么所有m个字符都匹配(然后停止)，要么在k>=0对字符成功匹配以后，遇到了一堆不匹配的字符。在后一种情况下，如果c是文本中的不匹配字符，我们从坏符号移动表的第c列取出单元格t©的值。如果k>0，还要从好后缀移动表中取出相应的d2的值。然后将模式沿着文本向右移动d个字符的距离，d是按照以下公式计算出来的：
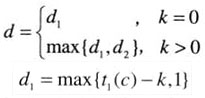
    Image Loading

一个例子：查找BAOBAB。
坏符号移动表
好后缀移动表
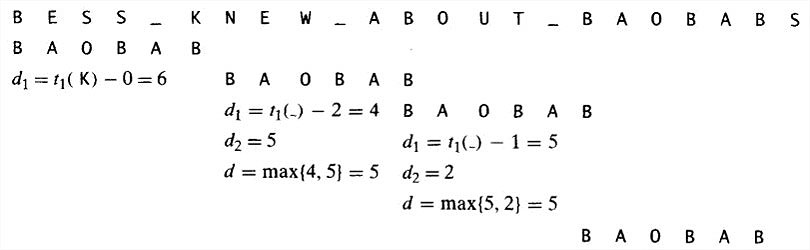
用Boyer-Moore算法进行字符串匹配的例子

1
2


散列法

散列是一种非常高效的实现字典的方法。它的基本思想是把键映射到一张一维表中。这种表在大小上的限制使得它必须采用一种碰撞解决机制。散列的两种主要类型是开散列(又称为分离链，键存储在散列表以外的链表中)以及闭散列(又称为开式寻址，键存储在散列表中)。平均情况下，这两种算法的查找、插入和删除操作的效率都是属于O(1)的。

开散列(分离链)

开散列中，键被存储在附着于散列表单元格上的链表中。每个链表包含着所有散列到该单元格的键。

用分离链构造散列表的例子

闭散列(开式寻址)

闭散列中，所有的键都存储在散列表本身。最简单的处理碰撞的策略是线性探查，它检查碰撞发生处后面的单元格。如果该单元格为空，新的键就放置在那里；如果下一个单元格也被占用了，就检查该单元格的直接后继是否可用，依次类推。到达末尾就从头开始。

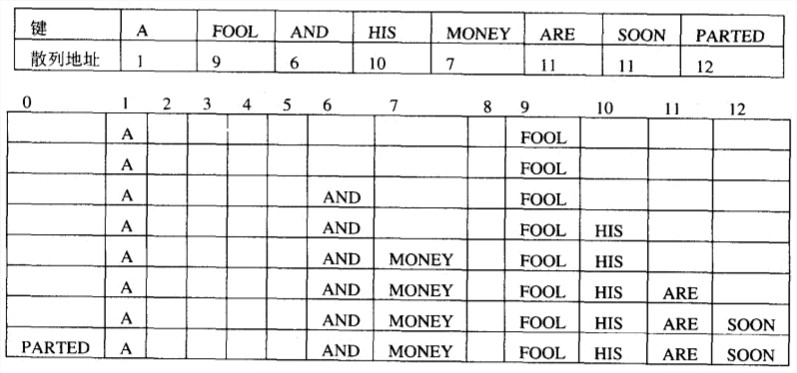
用线性探查构造散列表的例子
删除的时候需要“延迟删除”，即只标记，不删除。

相关题目

  1. 生日悖论。当一个房间里有多少人的时候，其中两个人生日(月和日)相同的概率大于1/2？
    解答：生日悖论的解答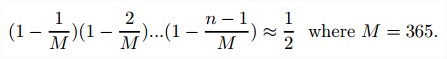
    第一个人有365/365个选择，第二个人有364/365种选择，…
    所以n约等于22.5。

  2. ADT字典的5种实现的平均效率类型。
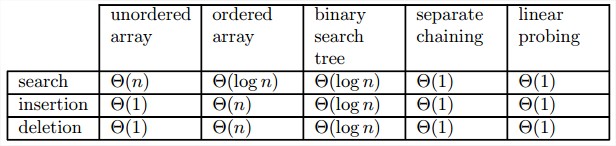
    Image Loading

B树

B树是一棵平衡查找树，它把2-3树的思想推广到允许多个键位于同一个节点上。它的主要应用是维护存储在磁盘上的数据的类索引信息。通过选择恰当的树的次数，即使对于非常大的文件，我们所实现的查找、插入和删除操作也只需要执行很少几次的磁盘存取。

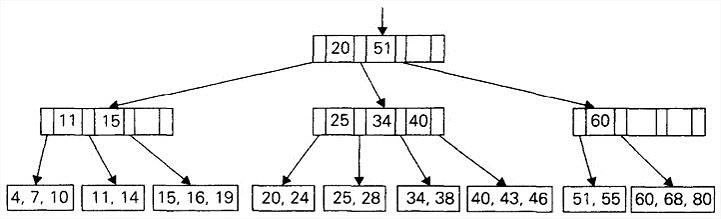
B树所有的数据记录(或者记录的键)都按照键的升序存储在叶子中。它们的父母节点作为索引。具体来说，每个父母节点包含n-1个有序的键K1<...<Kn−1K^1<...<K_{n-1}(假设它们是唯一的)。这些键之间插入了n个指向节点子女的指针，使得子树T0T_0中的所有键都小于K1K_1，子树T1T_1中的所有键都大于等于K1K_1小于K2K_2，而K1K_1等于子树T1T_1中最小的键，以此类推直到最后一棵子树。这样的一个节点称为n节点。
B树的父母节点，n节点

一棵次数为m⩾2m\geqslant2的B树必须满足下面这些结构上的特性：

  • 它的根要么是一个叶子，要么具有2到m个子女。
  • 除了根和叶子以外的每个节点，具有m/2到m个子女(因此也具有m/2-1)到m-1个键。
  • 这棵树是(完美)平衡的，也就是说，它的所有叶子都是在同一层上。

一棵次数为4的B树的例子
在上图的B树中插入65的结果

1
2
// B树中的键插入算法
// TODO

[1] 算法设计/与分析基础(第2版)