数值计算

深度学习花书第4章笔记。

深度学习 - 第4章 数值计算

机器学习算法通常需要大量的数值计算。这通常是指通过迭代过程更新解的估计值来解决数学问题的算法，而不是通过解析过程推导出公式来提供正确解的方法。常见的操作包括优化 (找到最小化或最大化函数值的参数) 和线性方程组的求解。对数学计算机来说，实数无法在有限内存下精确表示，因此仅仅是计算涉及实数的函数也是困难的。

上溢和下溢

舍入误差的累积可能导致巨大的错误。在实现深度学习算法时，底层库的开发者应该牢记数值问题。

• 下溢 underflow
  当接近零的数被四舍五入为零时发生下溢。许多函数在其参数为零而不是一个很小的正数时才会表现出质的不同。例如，我们通常要避免被零除或避免取零的对数。下一步运算会变成非数字。
• 上溢 overflow
  当大量级的数被近似为$\infty$或$-\infty$时发生上溢。进一步的运算通常会导致这些无限制变为非数字。

例子：softmax
常用于预测与 Multinouilli 分布相关联的概率。

$softmax(x) = \frac{\exp(x_i)}{\sum_{j=1}^n \exp(x_j)}$

假设所有$x_i$都等于$c$，按理说所有输出都应该为$\frac{1}{n}$。可如果$c$是很大的正数，$exp(c)$会上溢，导致表达式未定义。如果$c$是很小的负数，$exp(c)$会下溢，则分母为零，表达式未定义。
解决方法，计算 $softmax(z)$，$z = x - \max_i x_i$。函数值不会因为从输入向量减去或加上标量而改变。减去$max_i x_i$导致 exp 的最大参数为0，这排除了上溢。同样，分母中至少有一个值为1的项，排除了下溢。

病态条件

条件数指的是函数相对于输入的微小变化而变化的快慢程度。输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的，因为输入中的舍入误差可能导致输出的巨大变化。
考虑函数 $f(x) = A^{-1}x$。当 $A \in R^{n \times n}$ 具有特征值分解时，其条件数为

$\max_{i,j} |\frac{\lambda_i}{\lambda_j}|$

这是最大和最小特征值的模之比。当该数很大时，矩阵求逆对输入的误差特别敏感。

基于梯度的优化方法

大多数深度学习算法都涉及某种形式的优化。优化指的是改变 x 以最小化或最大化某个函数 f(x) 的任务。一般用最小化 f(x) 指代大多数最优化问题。
通常使用一个上标 * 来表示最小化或最大化函数的 x 值，如 $x^* = \arg \min f(x)$。

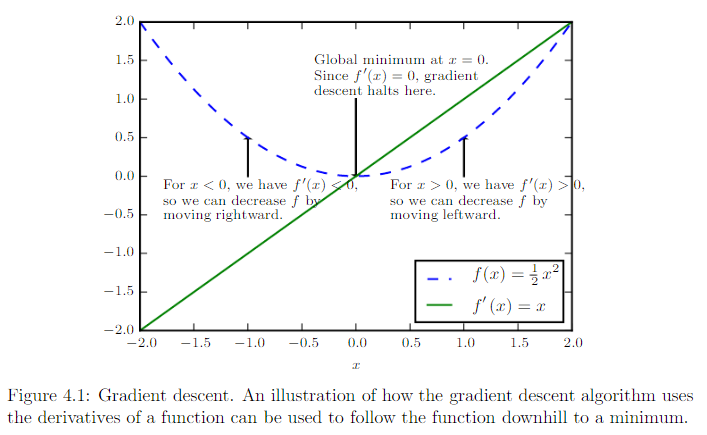
梯度下降 gradient descent 就是将 x 往导数的反方向移动一小步来减少 f(x)。
如果是多维，就是偏导数 partial derivative。梯度 gradient 是相对一个向量求导的导数：f 的导数是包含所有偏导数的向量，记为 $\triangledown_x f(x)$。梯度的第 i 个元素是 f 关于 $x_i$ 的偏导数。
梯度下降建议新的点为：$x' = x - \epsilon \triangledown_x f(x)$，$\epsilon$为学习率。

临界点的类型

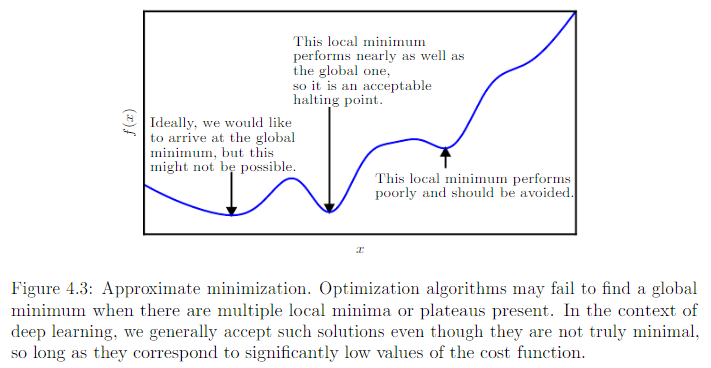
近似最小化

梯度之上：Jacobian 和 Hessian 矩阵

计算输入和输出都是向量的函数的所有偏导数，放在一个矩阵中，就是 Jacobian 矩阵。具体来说，如果我们有一个函数 $f: R^m \rightarrow R^n$，$f$ 的 Jacobian 矩阵 $J \in R^{n \times m}$ 定义为：

$J_{i,j} = \frac{\partial}{\partial x_j} f(x)_i$

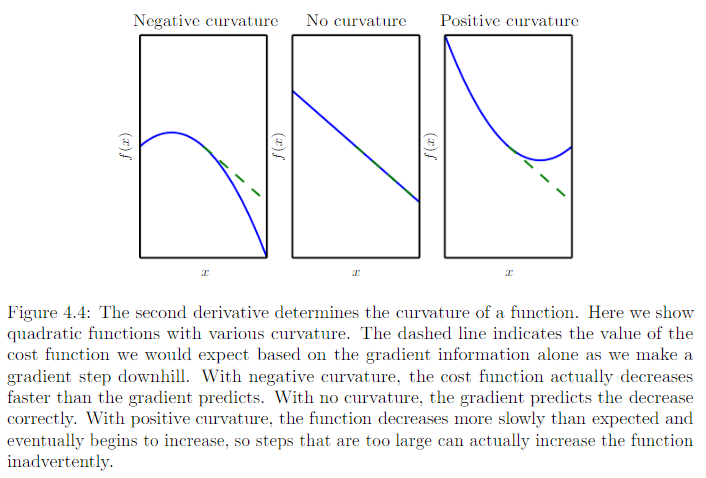
二阶导数，告诉我们一阶导数将如何随着输入的变化而变化。它表示只基于梯度信息的梯度下降步骤是否会产生如我们预期的那样大的改善。二阶导数是对曲率的衡量。

• 二阶导数为零。没有曲率，也就是一条平坦的线，仅用梯度就可以预测它的值。我们使用沿着负梯度方向大小为$\epsilon$的下降步，当该梯度是1时，代价函数将下降$\epsilon$。
• 二阶导数为负。函数曲线向下凹陷，向上凸出，因此代价函数将下降得比$\epsilon$多。
• 二阶导数为正。函数曲线向上凹陷，向下凸出，代价函数将下降得比$\epsilon$少。

当函数有多维输入时，二阶导数也很多，合并为一个矩阵，即 Hessian 矩阵。Hessian 矩阵定义为：

$H(f)(x)_{i,j} = \frac{\partial^2}{\partial x_i \partial x_j} f(x)$

Hessian 等价于梯度的 Jacobian 矩阵。

我们可以通过(方向)二阶导数预期一个梯度下降步骤能表现得多好。我们在当前点$x_{(0)}$处做函数$f(x)$的近似二阶泰勒级数：

$f(x) \approx f(x^{(0)}) + (x - x^{(0)})^T g + \frac{1}{2}(x - x^{(0)})^T H (x - x^{(0)})$

其中 $g$ 是梯度，$H$是$x^{(0)}$点的 Hessian。如果我们使用学习率$\epsilon$，那么新的点$x$将会是$x^{(0)} - \epsilon g$。代入上述的近似，可得：

$f(x^{(0)} - \epsilon g) \approx f(x^{(0)}) - \epsilon g^T g + \frac{1}{2} \epsilon^2 g^T H g$

其中有3项：函数的原始值、函数斜率导致的预期改善、函数曲率导致的校正。当最后一项太大时，梯度下降实际上是可能向上移动的。
当$g^T H g$为正时，计算可得使近似泰勒级数下降最多的最优步长为：

$\epsilon^* = \frac{g^Tg}{g^T H g}$

Hessian 的特征值决定了学习率的量级。

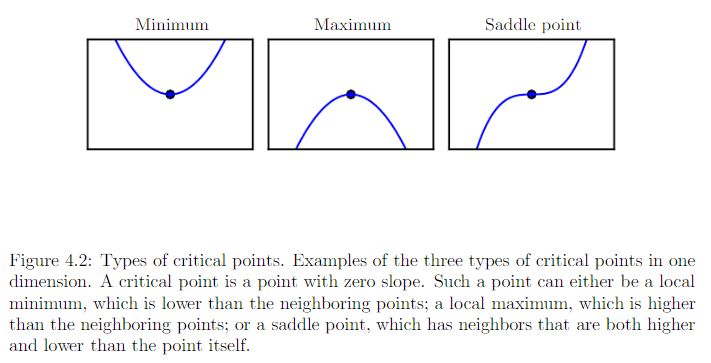
二阶导数还可以用于确定一个临界点是否是局部极大点、全局极小点、鞍点。临界点处 f’(x) = 0.

• f’’(x) > 0 或 Hessian 是正定的(所有特征值都是正的)
  f’(x) 会随着我们移向右边而增加，移向左边而减小。全局极小点。

• f’’(x) < 0 或 Hessian 是负定的
  局部极大点

• f’’(x) = 0
  不确定。x 可以是鞍点或平坦区域的一部分。

• 一阶优化算法 first-order optimization algorithms
  仅适用梯度信息的优化算法。如梯度下降。

• 二阶优化算法 second-order optimization algorithms
  使用 Hessian 矩阵的优化算法。如牛顿法。

梯度下降无法利用包含在 Hessian 矩阵中的曲率信息。

凸优化算法只对凸函数适用，即 Hessian 处处半正定的函数。因为这些函数没有鞍点而且其所有全局极小点必然是全局最小点。所以表现很好。
但是，深度学习中的大多数问题都难以表示成凸优化的形式。凸优化仅用作一些深度学习算法的子程序。

约束优化

限制了定义域，约束优化 constrained optimization。
可转化成原始优化问题的解。见拉格朗日算子。

Ref:
[1] 深度学习