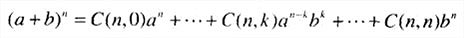动态规划
动态规划方法是一种对具有交叠子问题的问题进行求解的技术。一般来说,这样的子问题出现在求解给定问题的递推关系中,这个递推关系中包含了相同类型的更小子问题的解。动态规划法建议,与其对交叠的子问题一次又一次地求解,还不如对每个较小的子问题只解一次并把结果记录在表中,这样就可以从表中得出原始问题的解。
对一个最优问题应用动态规划方法要求该问题满足最优性原则:一个最优问题的任何实例的最优解是由该实例的子实例的最优解组成的。
计算二项式系数
通过构造帕斯卡三角形来计算二项式系数可以看作是动态规划技术在一个非最优问题上的应用。
二项式系数记作C(n,k),是来自于一个n元素集合的k元素组合(子集)的数量(0⩽k⩽n)。
二项式系数这个名字来源于这些数字出现在二项式公式之中。
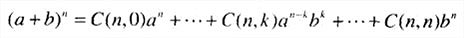
动态规划技术可以利用二项式系数的两个性质:
\mbox{当}n>k>0\mbox{时,}C(n,k)=C(n-1,k-1)+C(n-1,k)
C(n,0)=C(n,n)=1
计算过程是逐行从左到右填此表的过程。每行第一个为1,因为C(n,0)=1。每行最后一个数字为1,在主对角线上,C(i,i)=1。其他单元格根据性质是前一行前一列和前一行当前列的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <iostream>
#include <vector>
#include <string>
using namespace std;
int binomial(int n, int k)
{
if (k > n || k < 0 || n < 0) return 0;
vector<int> temp(k+1,0);
vector<vector<int> > C(n+1, temp);
for (int i = 0; i <= n; ++i)
{
for (int j = 0; j <= min(i,k); ++j)
{
if (j == 0 || j == i) {C[i][j] = 1;}
else{
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
}
return C[n][k];
}
int main()
{
cout << "C[5,3] = " << binomial(5,3) << endl;
system("Pause");
}
|
时间效率O(nk)。
相关题目
- 最短路径计算。国际象棋中的车可以水平或竖直移到棋盘中同行或同列的任何一个格子。一个车要从棋盘的一角移到对角的另一角,有多少种最短路径?
解答:可以得到递推公式:
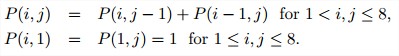
结果如图:
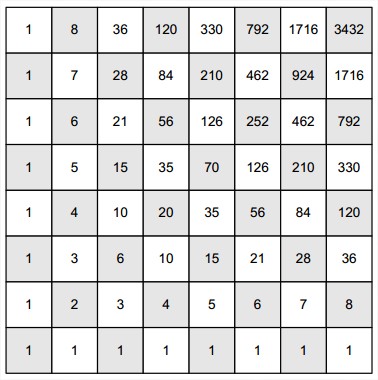
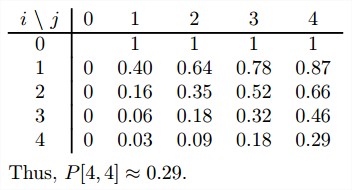
- 世界大赛的胜率。考虑A和B两支队伍,正在进行一系列比赛,直到一个队赢得了n场比赛为止。假设A队赢得每场比赛的概率都是相同的,即等于p,而A队丢掉比赛的概率是q=1-p(因此,就不存在平局了)。当A对还需要i场胜利才能赢得系列赛,B队还需要j场胜利才能赢得系列赛的时候,A队赢得系列赛的概率为P(i,j)。为P(i,j)建立一个可以在动态规划算法中使用的递推关系。如果A队赢得一场比赛的概率是0.4,该队赢得一个7场系列赛的概率是多少?
解答:考虑一场比赛。如果A以p的概率胜的话,A还需要i-1场才赢,B还需要j场才赢;如果A以1-p的概率输的话,A还需要i场才赢,B还需要j-1场赢。于是得到递推式:
P(i,j) = pP(i-1,j)+qP(i,j-1) \mbox{ for }i,j>0
初始状态是:
P(0,j)=1 \mbox{ for }j>0 \mbox{, }P(i,0)=0 \mbox{ for }i>0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include <iostream>
#include <vector>
#include <string>
using namespace std;
float world_series(int n, float p)
{
if (n < 1) return 1;
if (p <= 0) return 0;
vector<float> temp(n+1,0);
vector<vector<float> > P(n+1, temp);
for (int i = 1; i <= n; ++i)
{
P[i][0] = 0.0f;
}
for (int j = 1; j <= n; ++j)
{
P[0][j] = 1.0f;
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
P[i][j] = p * P[i-1][j] + (1-p) * P[i][j-1];
}
}
return P[n][n];
}
int main()
{
cout << "如果A队赢得一场比赛的概率是0.4,该队赢得一个7场系列赛的概率是:" << world_series(4,0.4f) << endl;
system("Pause");
}
|
Warshall算法和Floyd算法
Warshall算法
Warshall算法可以告诉我们给定图的顶点之间是否存在着任意长度的有向路径。
一个n顶点有向图的传递闭包可以定义为一个n阶布尔矩阵,如果从第i个顶点到第j个顶点之间存在一条有效的有向路径(即长度大于0的有向路径),矩阵第i行第j列的元素为1,否则tij=0。
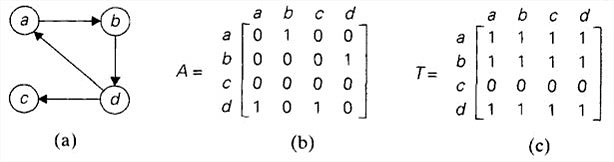
不同于DFS和BFS需要多次遍历计算传递闭包,Warshall算法通过一系列n阶布尔矩阵来构造。R0,...,Rk−1,Rk,Rn。分别表示i和j之间是否有长度不大于k的有向路径。所以R0就是有向图的邻接矩阵,之后每一个后继矩阵相对它的前驱来说,都允许增加一个顶点作为其路径上的顶点。序列中最后一个矩阵,反映了能够以有向图的所有n个顶点作为中间顶点的路径,因此它就是有向图的传递闭包。
对于如何从矩阵Rk−1的元素中生成矩阵Rk的元素,有下面的公式:
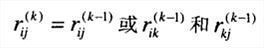
这个公式意味着以下规则:
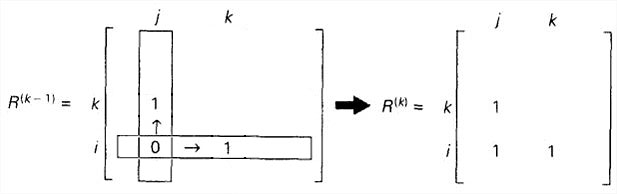
- 如果一个元素rij在Rk−1中是1,它在Rk中仍然是1。
- 如果一个元素rij在Rk−1中是0,当且仅当矩阵中第i行第k列的元素和第k行第j列的元素都是1,该元素在Rk中才能变成1。如图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include <iostream>
#include <vector>
#include <algorithm>
#include <iterator>
using namespace std;
//---------------------------------------------------
class MAT
{
public:
MAT(int n){vector<bool> temp(n,false); m_inner.assign(n, temp);}
void set_value(int m, int n, bool val) {m_inner[m-1][n-1] = val;}
bool get_value(int m, int n) {return m_inner[m-1][n-1];}
int get_size() {return m_inner.size();}
void print()
{
for_each(m_inner.begin(), m_inner.end(),
[](const vector<bool>& val)
{
copy(val.begin(), val.end(), ostream_iterator<int>(cout, " "));
cout << endl;
});
}
protected:
vector<vector<bool> > m_inner;
};
//---------------------------------------------------
void warshall(MAT& A)
{
// 实现计算传递闭包的Warshall算法
// 输入:包括n个顶点有向图的邻接矩阵A
// 输出:该有向图的传递闭包
int n(A.get_size());
MAT temp(A);
for (int k = 1; k <= n; ++k)
{
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
bool val(A.get_value(i,j) | (A.get_value(i,k)&A.get_value(k,j)));
temp.set_value(i, j, val);
}
}
A=temp;
cout << "Process: " << k << endl;
A.print();
}
}
//---------------------------------------------------
int main()
{
MAT matrix(4);
matrix.set_value(1,2,true);
matrix.set_value(2,4,true);
matrix.set_value(4,1,true);
matrix.set_value(4,3,true);
cout << "Original:" << endl;
matrix.print();
warshall(matrix);
cout << "Warshall:" << endl;
matrix.print();
system("Pause");
}
|
计算完全最短路径的Floyd算法
给定一个有向或无向的加权连通图,完全最短路径问题要求找到从每个顶点到其他所有顶点之间的距离(最短路径的长度)。
可以把最短路径的长度记录在一个称为距离矩阵的n阶矩阵D中:矩阵中第i行第j列的元素dij指出了从第i个顶点到第j个顶点之间最短路径的长度。
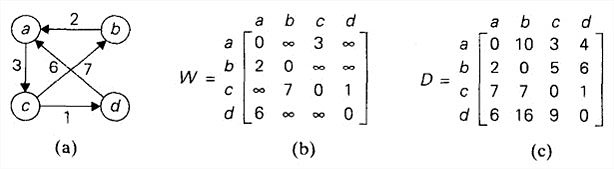
Floyd算法用一种类似Warshall方法的算法来生成这个距离矩阵。它通过一系列n阶矩阵来计算一个n顶点加权图的距离矩阵。D0,...,Dk−1,Dk,...,Dn。分别表示i和j之间长度不大于k的最短路径。所以D0就是有向图的权重矩阵,之后每一个后继矩阵相对它的前驱来说,都允许增加一个中间顶点。序列中最后一个矩阵,反映了能够以图的所有n个顶点为中间顶点的最短路径,就是图的距离矩阵。
Floyd算法的内在思想是两条路径的比较:一条路径不把第k个顶点作为中间顶点,另一条路径反之。第一条路径所包含的中间顶点的编号不会大于k-1。第二条路径包含两段子路径,一条从i到k,一条从k到j,路径中每个中间顶点的编号都不大于k-1。
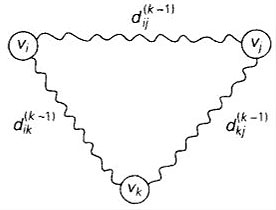
取其中更短的那条,得到递推式:
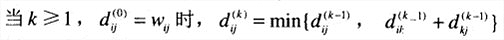
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| #include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
//---------------------------------------------------
class MAT
{
public:
MAT(int n){vector<int> temp(n,INT_MAX); m_inner.assign(n, temp);}
void set_value(int m, int n, int val) {m_inner[m-1][n-1] = val;}
int get_value(int m, int n) {return m_inner[m-1][n-1];}
int get_size() {return m_inner.size();}
void print()
{
for_each(m_inner.begin(), m_inner.end(),
[](const vector<int>& val)
{
for_each(val.begin(), val.end(), [](int v) {
if (v == INT_MAX)
{
cout << "N" << " ";
}else
{
cout << v << " ";
}
});
cout << endl;
});
}
protected:
vector<vector<int> > m_inner;
};
//---------------------------------------------------
void floyd(MAT& W)
{
MAT D(W);
int n(W.get_size());
for (int k = 1; k <= n; ++k)
{
D = W;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
int v1(D.get_value(i,k));
int v2(D.get_value(k,j));
int val(INT_MAX);
if (v1 != INT_MAX && v2 != INT_MAX)
{
val = min(D.get_value(i,j), v1+v2);
}else
{
val = D.get_value(i,j);
}
W.set_value(i,j, val);
}
}
cout << "Process: " << k << endl;
W.print();
}
}
//---------------------------------------------------
int main()
{
MAT matrix(4);
matrix.set_value(1,1,0);
matrix.set_value(2,2,0);
matrix.set_value(3,3,0);
matrix.set_value(4,4,0);
matrix.set_value(1,3,3);
matrix.set_value(2,1,2);
matrix.set_value(3,2,7);
matrix.set_value(3,4,1);
matrix.set_value(4,1,6);
cout << "Original:" << endl;
matrix.print();
floyd(matrix);
system("Pause");
}
|
相关题目
- 假设矩阵的行是由比特串来表示的,可以对它执行位或操作,重写Warshall算法。
- 加强Floyd算法,使得该算法能够求出最短路径本身,而不仅仅是长度。
- 挑游戏棒。该游戏中有若干塑料或木制的游戏棒散倒在桌子上,玩家要试着把它们一根接一根取走而不要移动其他游戏棒。在这里,我们只考虑一对对游戏棒之间是不是通过一系列相互搭着的游戏棒相连接。给定n(n>1)根游戏棒(假设它们散倒在一张很大的画图纸上)的端点列表,请找出所有相连的游戏棒。请注意,搭在一起的算相连,而能通过其他相连游戏棒间接相连的也应该算相连。
最优二叉查找树
如果已知键的一个集合以及它们的查找概率,可以使用动态规划方法来构造一棵最优二叉查找树。
包含n个键的二叉查找树的总数量等于第n个卡塔兰数:
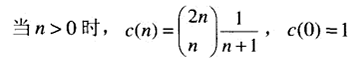
它以4n/n1.5的速度逼近无穷大。所以通过穷举寻找最优二叉查找树的想法是不现实的。
用动态规划的方法:
定义
设a1,…,an是从小到大排列的互不相等的键,p1,…,pn是它们的查找概率。Tij是由键ai,…,aj构成的二叉树,C[i,j]是在这棵树中成功查找的最小的平均查找次数,其中i,j是一些整数下标,1⩽i⩽j⩽n。我们最终要求得的是C[1,n]。
为了求得递推式,考虑以ak为根,左右皆是最优排列的子树,如图:
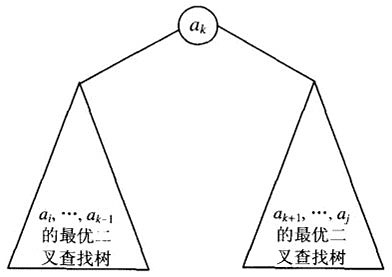
递推式
可以得到如图的递推关系。即min{(p*第一层) + (p*(在左子树的层数 + 第一层)) + (p*(在右子树的层数 + 第一层))},即min(根+左+右)。

运算过程
计算C[i,j]时需要用到的值有:i行中位于j列左边的列中的值,j列中在i行下边的行中的值。箭头指出了需要对元素求和的一对对单元格,然后求出这些元素对的和的最小值,把它作为C[i,j]的值记录下来。
要沿着表格的对角线填写表格,一开始把主对角线全部填0,然后把给定概率pi(1⩽i⩽n)填在对角线的右上方,并沿着右上角移动。
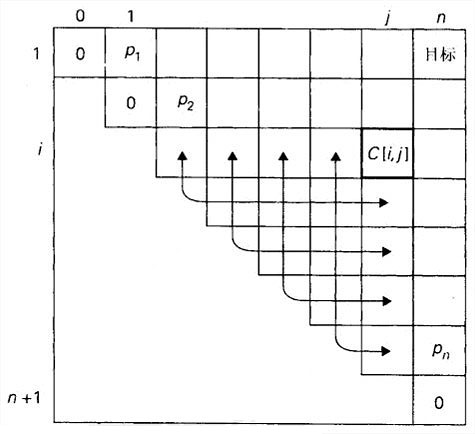
之前描述的算法是计算C[1,n]的,也就是最优二叉树中成功查找的平均比较次数。如果想得到最优二叉树本身,需要维护另一个二维表来记录k值。
一个例子:对以下4个键应用本算法。

![初始表格以及计算C[1,2]](/img/best_bst_example_step1.jpg)
依次计算,最后得到这两个表:
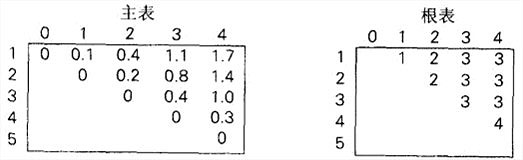
所以,平均键值比较次数是1.7。因为R[1,4]=3,最优树的根为C;因为R[1,2]=2,左子树的根为2。得到如下的最优树:
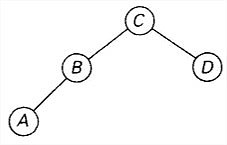
背包问题和记忆功能
背包问题
给定n个重量为w1,...,wn,价值为v1,...,vn的物品和一个承重量为W的背包,求这些物品中最有价值的一个子集,并且要能够装到背包中。
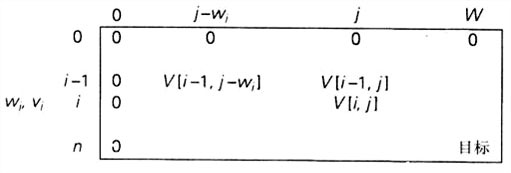
动态规划算法需要有递推式。考虑一个由前i个物品(1⩽i⩽n)定义的实例,物品的重量分别为w1,...,wi,价值分别为v1,...,vi,背包的承重量为j(1⩽j⩽W)。设V[i,j]为该实例的最优解的物品总价值,也就是说,是能够放进承重量为j的背包中的前i个物品中最有价值子集的总价值。可以把前i个物品中能够放进承重量为j的背包中的子集分成两个类别:包括第i个物品的子集和不包括第i个物品的子集。然后有下面的结论:
- 根据定义,在不包括第i个物品的子集中,最优子集的价值是V[i−1,j]。
- 在包括第i个物品的子集中(因此,j−w⩽0),最优子集是由该物品和前i−1个物品中能够放进承重量为j−wi的背包的最优子集组成。这种最优子集的总价值等于vi+V[i−1,j−wi]。
可以得到递推式:

我们的目标是求V[n,W]。
一个例子:
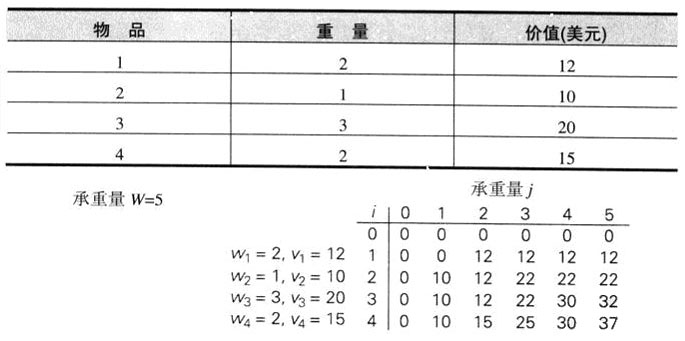
最大的总价值为V[4,5]=37。
可以通过回溯这个表格单元的计算过程来求得最优子集的组成元素。因为V[4,5]≠V[3,5],物品4以及填满背包余下5-2=3个单位承重量的每一个最优子集都包括在最优解中。而后者是由元素V[3,3]来表示的。因为V[3,3]=V[2,3],物品3不是最优子集的一部分。因为V[2,3]≠V[1,3],物品2是最优子集的一部分。V[1,2]≠V[0,2],物品1也是最优子集的一部分。即{物品1,物品2,物品4}。
记忆功能
记忆功能技术试图把自顶向下和自底向上方法的优势结合起来,对具有交叠子问题的问题求解。它用自顶向下的方式,对给定问题的必要子问题只求解一次,并把它们的解记录在表中。
记忆功能只对必要的子问题求解并且只解一次。该方法用自顶向下的方式对给定的问题求解,但还需要维护一个类似自底向上动态规划算法使用的表格。一开始的时候,用一种NULL符号初始化表中所有的单元格,用来表明它们还没有被计算过。然后,一旦需要计算一个新的值,该方法首先检查表中相应的单元格。如果该单元格不是NULL,它就简单地从表中取值;否则,就使用递归调用进行计算,然后把返回的结果记录在表中。
对背包问题用此方法求解
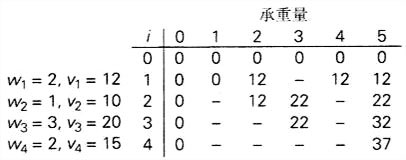
相关问题
- 为最优二叉查找树问题写一段记忆功能的代码(我们可以把功能限制在求成功查找中的最少键值比较次数)。
- 为找零问题设计一个动态规划算法:给定金额n以及各种面额d1,d2,...,dn的数量无限的硬币,求总金额等于n的硬币的最少个数,或者指出该问题无解。
leetcode相关题目
Triangle
Maximum Subarray
Palindrome Partitioning II
Maximal Rectangle
Best Time to Buy and Sell Stock III
Interleaving String
Scramble String
Minimum Path Sum
Edit Distance
Decode Ways
Distinct Subsequences
Word Break
Word Break II
[Backtracing & Branch-and-Bound] | Palindrome Partitioning
[Backtracing & Branch-and-Bound] | Unique Paths
[Backtracing & Branch-and-Bound] | Unique Paths II
[Greedy Technique] | Jump Game
[Tree] | Unique Binary Search Trees
[1] 算法设计与分析基础(第2版)
[2] leetcode

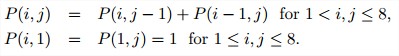



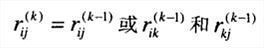



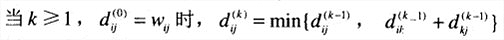
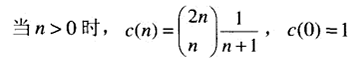




![初始表格以及计算C[1,2]](/img/best_bst_example_step1.jpg)