Big-O Notation

A Stellar Hiker

2014-12-19

Algorithm

刷题的时候发现不会计算递归算法时间复杂度，集中总结一下。

时间复杂度是随问题规模n增大，算法执行时间的增长率。英文书中有时称为Big-O。
Big-O notation expresses the runtime of an algorithm as a function of a given input of size n.

典型的时间复杂度

类型	名称	注释
常量Constant	$O(1)$	为数很少的效率最高的算法。
对数Logarithmic	$O(log(n))$	一般来说，算法的每一次循环都会消去问题规模的一个常数因子。注意，一个对数算法不可能关注它的输入的每一个部分(哪怕是输入的一个固定部分)：任何能做到这一点的算法最起码拥有线性运行时间。
线性Linear	$O(n)$	扫描规模为n的列表(例如顺序查找)的算法属于这个类型。
n-log-n	$O(n*log(n))$	许多分治算法，包括合并排序和快速排序的平均效率，都属于这个类型。
平方Quadratic	$O(n^2)$	一般来说，这是包含两重嵌套循环的算法的典型效率。基本排序算法和n阶方阵的某些特定操作都是标准的例子。
立方Cubical	$O(n^3)$	一般来说，这是包含三重嵌套循环的算法的典型效率。线性代数中的一些著名算法属于这一类型。
指数Exponential	$O(2^n)$	求n个元素集合的所有子集的算法是这种类型的典型例子。“指数”这个术语常常被用在一个更广的层面上，不仅包括这种类型，还包括那些增长速度更快的类型。
阶乘Factorial	$O(n!)$	求n个元素集合的完全排列的算法是这种类型的典型例子。

注意时间复杂度计算中常常省略一些级数小的因数，比如常数因数。

对各种级数的感性认识

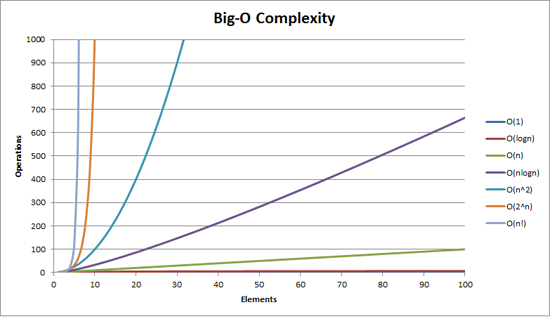
big-o-notation

计算方法

分析非递归算法效率的通用方案

决定用哪个(哪些)参数表示输入规模。即决定n。
找出算法的基本操作(作为一个规律，它总是位于算法的最内层循环中)。
检查基本操作的执行次数是否只依赖输入规模。如果它还依赖一些其他的特性，则最差效率、平均效率以及最优效率(如有必要)需要分别研究。
建立一个算法基本操作执行次数的求和表达式。
利用求和运算的标准公式和法则来建立一个操作次数的闭合公式，或者至少确定它的增长次数。
等差数列求和公式： $S_n=\frac{(a_1+a_n)n}{2}$
等比数列求和公式： $S_n=\frac{a_1(1-q^n)}{(1-q)} (q\neq1)$

例子

// 求一个十进制正整数在二进制表示中的二进制数字个数。
int count_binary(int n)
{
    // input: 十进制正整数n
    // output: n在二进制表示中的二进制数字个数
    int count(1);
    while (n > 1)
    {
        ++count;
        n /= 2;
    }
    return count;
}

本算法最频繁的操作是决定是否继续执行循环体的比较运算n > 1。
在循环每次执行过程中，n的值基本都会减半，所以次数大约是 $log_2n$ 。

分析递归算法效率的通用方案

决定用哪个(哪些)参数作为输入规模的度量。
找出算法的基本操作。
检查一下，对于相同规模的不同输入，基本操作的执行次数是否可能不同。如果有这种可能，则必须对最差效率、平均效率以及最优效率做单独研究。
对于算法基本操作的执行次数，建立一个递推关系以及相应的初始条件。
解这个递推式，或者至少确定它的解的增长次数。
- 反向替换法。如：
  $M(n) = M(n-1)+1$ 替换 $M(n-1)=M(n-2)+1$
  $= (M(n-2)+1)+1 = M(n-2)+2$ 替换 $M(n-2)=M(n-3)+1$
  $= (M(n-3)+1)+2 = M(n-3)+3$
  得到： $M(n) = M(n-1)+1=...=M(n-i)+i=...=M(n-n)+n=n$
- 或者使用特征方程(略)。

例子

// 求一个十进制正整数在二进制表示中的二进制数字个数。
int count_binary(int n)
{
    // input: 十进制正整数n
    // output: n在二进制表示中的二进制数字个数
    if (n == 1) {return 1;}
    else {return count_binary(n / 2) + 1;}
}

得到递推式与初始条件：
$A(n) = A(n/2)+1, n>1$
$A(1)=0$
使用平滑规则定理，在一个非常宽泛的假设下，无论n取何值，它的增长次数与 $n=2^k$ 时的增长次数是完全相同的。于是仅在 $n=2^k$ 的情况下对该递推式求解。
$A(2^k)=A(2^{k-1})+1, k>0$
$A(2^0)=0$
使用反向替换法就不再有困难了。
$A(2^k)=A(2^{k-1})+1$
$=(A(2^{k-2})+1)+1=A(2^{k-2})+2$
$=(A(2^{k-3})+1)+2=A(2^{k-3})+3$
$...$
$=A(2^{k-i})+i$
$=A(2^{k-k})+k$
得到 $A(2^k)=A(1)+k=k$
转换为原来的变量n的函数。因为 $n=2^k$ ，所以 $k=log_2n$ 。
$A(n)=log_2n \in O(logn)$

[1]: The C++ Standard Library 2nd Edition, P10-11
[2]: 算法设计与分析基础, P32-58